Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D

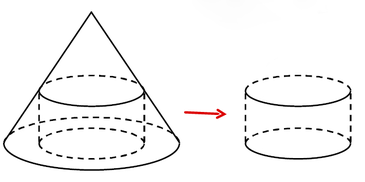
Xét mặt cắt và lấy các điểm như hình vẽ bên cạnh.
Theo đề thì O A = O B = r = 30 cm và O H = h = 120 cm
Đặt O C = O D = R là bán kính đường tròn đáy của khúc gỗ khối trụ thì:
E C O H = A C O A = O A − O C O A ⇔ E C h = r − R R ⇔ E C = 4 30 − R
Thể tích khúc gỗ khối trụ là
V = π R 2 . E C = 4 π . R 2 . 30 − R ⇒ f R = 30 R 2 − R 3
Xét hàm số f R trên 0 ; 30 ⇒ max f R = 4000
Vậy thể tích lớn nhất của khối trụ V = 0 , 016 m 3

Đáp án A
Chu vi đường tròn C = 2 π r ⇒ 2 π r = 14 c m ⇒ r = 7 c m
Xét khối món có thể tích V = 1 3 π r 2 h = 343 3 π c m 3 ⇒ h = 7 c m
Khối cầu được almf từ khối nón có bán kính mặt cầu lớn nhất khi khối cầu nội tiếp khối nón
Khi đó bán kính khối cầu (S) là R S = r . h r + r 2 + h 2 = 7 − 1 + 2 c m
Vậy diện tích lớn nhất cần tính là:
S = 4 π R 2 = 196 π 3 − 2 2 c m 2

Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.

Chọn đáp án C
Phương pháp
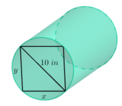
Tỉ số k = V 1 V 2 lớn nhất khi và chỉ khi V 2 lớn nhất. Khi đó hình trụ có chiều cao bằng cạnh của hình lập phương và có đường tròn đáy nội tiếp một mặt của hình lập phương.
Cách giải
Gọi a là cạnh của hình lập phương, khi đó thể tích của hình lập phương là V 1 = a 3 . Khi đó tỉ số k = V 1 V 2 lớn nhất khi và chỉ khi V 2 lớn nhất.
Khi đó hình trụ có chiều cao bằng cạnh của hình lập phương và có đường tròn đáy nội tiếp một mặt của hình lập phương







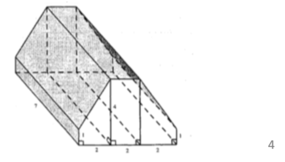
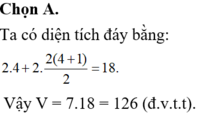
Đáp án D
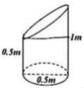
Gọi r 0 ; h 0 lần lượt là bán kính đáy và chiều cao của khối trụ.
Theo giả thuyết, ta có:
r 0 r = h − h 0 h ⇔ r 0 = 30. 120 − h 0 120 = 30 − h 0 4
Suy ra thể tích khối trụ là:
V = π r 0 2 . h 0 = π 30 − h 0 4 2 . h 0 = π . 120 − h 0 2 . h 0 16
Xét hàm số f t = t 120 − t 2 với t ∈ 0 ; 120 suy ra: max 0 ; 120 f t = 256000
Vậy thể tích lớn nhất của khối trụ là:
V max = π 256000 16 . 1 100 3 = 0 , 016 π c m 3