Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

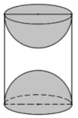
Khối cầu khoét đi có đường tròn lớn trùng với đáy hình trụ nên hai khối cầu có bán kính bằng bán kính trụ và bằng 1.
Thể tích khối trụ ban đầu là V = 1 2 . π . 2 = 2 π
Thể tích phần khoét đi là 2 nửa bán cầu, tức là 1 khối cầu có bán kính 1, có thể tích là
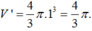
Thể tích phần còn lại của khối gỗ là
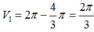
Vậy tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là
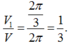
Chọn C.

Đáp án C
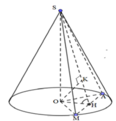
Phương pháp: Xác định góc giữa hai mặt phẳng α ; β :
- Tìm giao tuyến ∆ của α ; β
- Xác định 1 mặt phẳng γ ⊥ △
- Tìm các giao tuyến a = α ∩ γ , b = β ∩ γ
- Góc giữa hai mặt phẳng α ; β : α ; β = a;b
Cách giải: Kẻ OH ⊥ AM, H ∈ AM, OK ⊥ SH, K ∈ SH
Vì 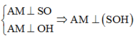
=> AM ⊥ OK
Mà OK ⊥ SH => OK ⊥ (SAM) => d(O;(SAM)) = OK = 2
Ta có: 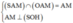 ( vì AM
⊥
OH, AM
⊥
SO)
( vì AM
⊥
OH, AM
⊥
SO)
Mà (SOH) ∩ (OAM) = OH; (SOH) ∩ (SAM) = SH => ((SAM);(OAM)) = (SH;OH) = S H O ^ = 30 0
Tam giác OHK vuông tại K
![]()
Tam giác SOH vuông tại O
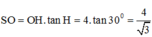
Tam giác OAM cân tại O, A O M ^ = 60 0 , OH ⊥ AM
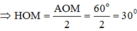
Tam giác OHM vuông tại H
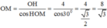
Thể tích khối nón: 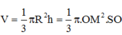
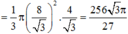

Đáp án A.
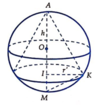
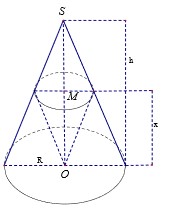
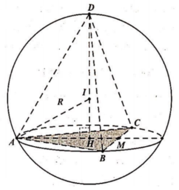
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A

Chọn đáp án A
Gọi I là tâm của hình tròn (C) và S là đỉnh của hình nón. Gọi bán kính của hình tròn (C) là r thì
![]()
Trường hợp 1: O nằm giữa S và I.
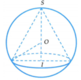
Chiều cao của hình chóp là SI = SO + OI = x + 6 (cm).
Thể tích khối chóp là V = 1 3 π 36 - x 2 x + 6 cm 3
Xét hàm số f x = 36 - x 2 x + 6 với 0 ≤ x < 6
Ta có f ' x = - 3 x 2 - 12 x + 36
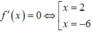
Do 0 ≤ x < 6 nên x = - 6.
Lập bảng biến thiên của hàm số ta thấy f(x) ta thấy f x ≤ f 2 = 256
Suy ra V ≤ V 1 = 1 3 π . 256 = 256 3 π cm 3
Dấu “=” xảy ra x = 2.
Trường hợp 2: I nằm giữa S và O
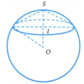
Chiều cao của hình chóp là SI = SO – OI = 6 – x (cm)
Thể tích của khối chóp là V = 1 3 π 36 - x 2 6 - x cm 3 (cm3).
Xét hàm số g x = 36 - x 2 6 - x với 0 ≤ x < 6
Ta có g ' x = 3 x 2 - 12 x - 36 < 0 , ∀ x ∈ 0 ; 6 nên hàm số g(x) nghịch biến trên 0 ; 6 .
Suy ra g x ≤ g 0 = 216
Khi đó V ≤ V 2 = 72 π cm 3 .
Dấu “=” xảy ra khi x = 0.
So sánh hai trường hợp 1 và 2, suy ra thể tích lớn nhất của khối chóp đã cho là V = 256 3 π cm 3 khi x = 2 c m .
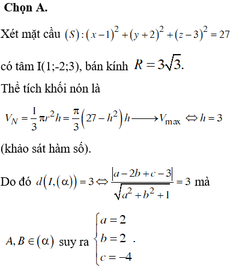


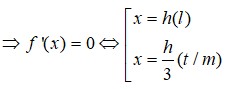



Đáp án A
Chu vi đường tròn C = 2 π r ⇒ 2 π r = 14 c m ⇒ r = 7 c m
Xét khối món có thể tích V = 1 3 π r 2 h = 343 3 π c m 3 ⇒ h = 7 c m
Khối cầu được almf từ khối nón có bán kính mặt cầu lớn nhất khi khối cầu nội tiếp khối nón
Khi đó bán kính khối cầu (S) là R S = r . h r + r 2 + h 2 = 7 − 1 + 2 c m
Vậy diện tích lớn nhất cần tính là:
S = 4 π R 2 = 196 π 3 − 2 2 c m 2