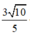Khoảng cách từ điểm M(1;-1) đến đường thẳng Δ: 3x + y + 4 = 0 là:
A. 2 10
B. 3 10 5
C. 5 2
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo bài ra ta có: quãng đường AB dài 540km => Nửa quãng đường AB dài 270km.
Gọi quãng đường ô tô và xe máy đã đi là S1 và S2.
Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc.
\(\dfrac{S_1}{V_1}=\dfrac{S_2}{V_2}=t\)
Ta có phương trinh:
\(\dfrac{270-a}{65}=\dfrac{270-a}{40}\Rightarrow t=\dfrac{270}{90}=3h\)
Vậy sau 3 giờ thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách xe máy đến M

Đồ thị hàm nhận \(x=1\) là tiệm cận đứng
Gọi \(M\left(a;b\right)\Rightarrow b=\dfrac{2a+1}{a-1}\)
Khoảng cách từ M đến trục hoành: \(\left|y_M\right|=\left|b\right|\)
Khoảng cách từ M đến tiệm cận đứng: \(\left|x_M-1\right|=\left|a-1\right|\)
Ta được hệ: \(\left\{{}\begin{matrix}b=\dfrac{2a+1}{a-1}\\\left|b\right|=\left|a-1\right|\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(0;-1\right);\left(4;3\right)\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(0;-1\right)\\M\left(4;3\right)\end{matrix}\right.\)

Trả lời:
Từ điền số 1 đến điểm 101 sẽ có: 101-1=100 khoảng bằng nhau.=> mỗi một khoảng bằng nhau có độ dài= 1m/100= 100cm/100=1cm
Từ điểm 13 đến điểm 31 có (31-13)=18 khoảng bằng nhau
=> Khoảng cách từ điểm 13 đến điểm 31 là: 18x1 cm= 18cm

M m ; 2 m + 1 m - 1 ∈ C m ≠ 1
Tiệm cận đứng x = 1 và tiệm cận ngang y = 2
Yêu cầu bài toán
⇔ a - 1 = 3 2 a + 1 a - 2 - 2 ⇔ a = 4 ⇒ M 4 ; 3 a = - 2 ⇒ M - 2 ; 1
Đáp án C
Chọn B.
Vậy khoảng cách từ điểm M(1;-1) đến đường thẳng Δ: 3x + y + 4 = 0 là