Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ điểm M (-2; 1) đến đường thẳng Δ là:
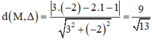
Khoảng cách từ điểm O (0; 0) đến đường thẳng Δ là:
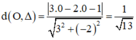

Câu 2:
c/ DO M thuộc \(\Delta\) nên tọa độ M có dạng \(M\left(a;\frac{1-3a}{2}\right)\)
Áp dụng công thức khoảng cách:
\(\frac{\left|5a-\frac{3\left(1-3a\right)}{2}+2\right|}{\sqrt{5^2+3^2}}=5\)
\(\Leftrightarrow\left|13a+1\right|=10\sqrt{34}\)
\(\Leftrightarrow\left[{}\begin{matrix}13a+1=10\sqrt{34}\\13a+1=-10\sqrt{34}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=\frac{-1+10\sqrt{34}}{13}\\a=\frac{-1-10\sqrt{34}}{13}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(\frac{-1+10\sqrt{34}}{13};\frac{8-15\sqrt{34}}{13}\right)\\M\left(\frac{-1-10\sqrt{34}}{13};\frac{8+15\sqrt{34}}{13}\right)\end{matrix}\right.\)
d/ Chẳng hiểu đề câu d là gì luôn? Cái gì bằng 2 lần khoảng cách từ N đến d bạn
Câu 2:
a/ Khoảng cách:
\(d\left(A;\Delta\right)=\frac{\left|3.5+2.4-1\right|}{\sqrt{3^2+2^2}}=\frac{22\sqrt{13}}{13}\)
b/ Gọi \(M\left(x;y\right)\) là 1 điểm thuộc đường phân giác
\(\Rightarrow d\left(M;\Delta\right)=d\left(M;d\right)\)
\(\Rightarrow\frac{\left|3x+2y-1\right|}{\sqrt{3^2+2^2}}=\frac{\left|5x-3y+2\right|}{\sqrt{5^2+3^2}}\)
\(\Leftrightarrow\sqrt{34}\left|3x+2y-1\right|=\sqrt{13}\left|5x-3y+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{34}\left(3x+2y-1\right)=\sqrt{13}\left(5x-3y+2\right)\\\sqrt{34}\left(3x+2y-1\right)=-\sqrt{13}\left(5x-3y+2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(3\sqrt{34}-5\sqrt{13}\right)x+\left(2\sqrt{34}+3\sqrt{13}\right)y-\sqrt{34}-2\sqrt{13}=0\\\left(3\sqrt{34}+5\sqrt{13}\right)x+\left(2\sqrt{34}-3\sqrt{13}\right)y-\sqrt{34}+2\sqrt{13}=0\end{matrix}\right.\)

Lấy điểm M( x0; 1-2x0) nằm trên d.
Từ giả thiết ta có:
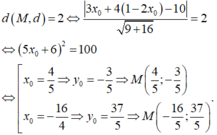
Chọn C.
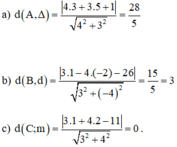

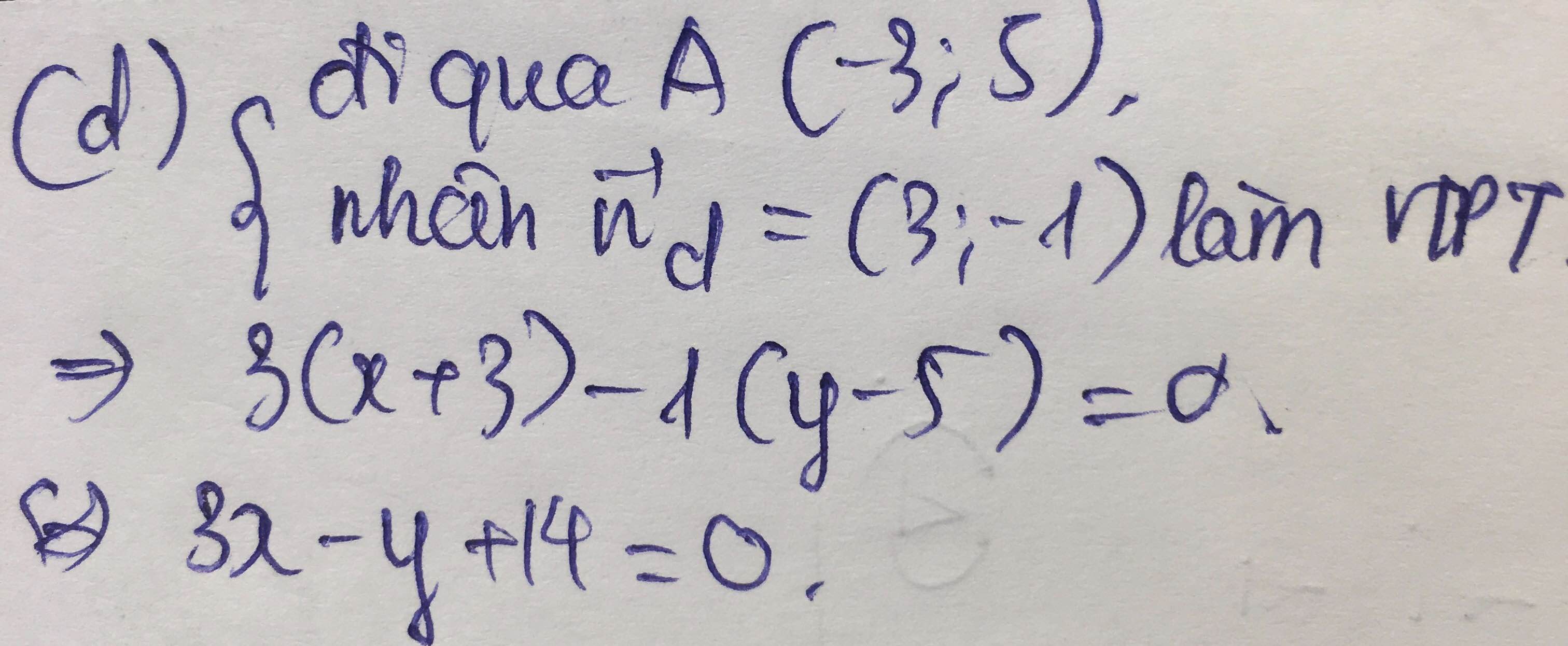


Chọn B.
Vậy khoảng cách từ điểm M(1;-1) đến đường thẳng Δ: 3x + y + 4 = 0 là