Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng công thức khoảng cách ta có
3. − 2 − 4.1 + 2 3 2 + − 4 2 = m − 2 + 3.1 − 3 m 2 + 3 2
⇔ 8 5 = − 2 m m 2 + 9 ⇔ 8 m 2 + 9 = 10 m ⇔ 64 ( m 2 + 9 ) = 100 m 2 ⇔ 64 m 2 + 576 = 100 m 2 ⇔ 36 m 2 = 576 ⇔ m 2 = 16 ⇔ m = ± 4
Đáp án là phương án C.
Chú ý. Học sinh có thể thử lại các phương án được đưa ra để chọn đáp án đúng, tuy nhiên sẽ tốn nhiều thời gian hơn là làm bài toán trực tiếp.

M thuộc (d1) nên M(1-2t;1+t)
Theo đề, ta có: d(M;d2)=d(M;d3)
=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)
=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|
=>|-2t+3|=|-11t+3|
=>-2t+3=-11t+3 hoặc -2t+3=11t-3
=>t=0 hoặc t=6/13
=>M(1;1); M(1/13; 19/13)

a: Vì M nằm trên d1 nên M(x;-x-2)
Theo đề, ta có: \(\dfrac{\left|x\cdot1-3\cdot\left(-x-2\right)+1\right|}{\sqrt{1^2+\left(-3\right)^2}}=3\)
\(\Leftrightarrow\left|x+3x+6+1\right|=3\sqrt{10}\)
\(\Leftrightarrow\left|4x+7\right|=3\sqrt{10}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3\sqrt{10}-7}{4}\\x=\dfrac{-3\sqrt{10}-7}{4}\end{matrix}\right.\)

Để hai đường thẳng song song thì:
m 2 = 2 m − 2 3 ≠ − m + 6 1 ⇔ m 2 = 2 m − 2 3 m 2 ≠ − m + 6 1 ⇔ 3 m = 4 m − 4 m ≠ − 2 m + 12 ⇔ m = 4 m ≠ 4
không tồn tại m thỏa mãn yêu cầu bài toán.
ĐÁP ÁN D

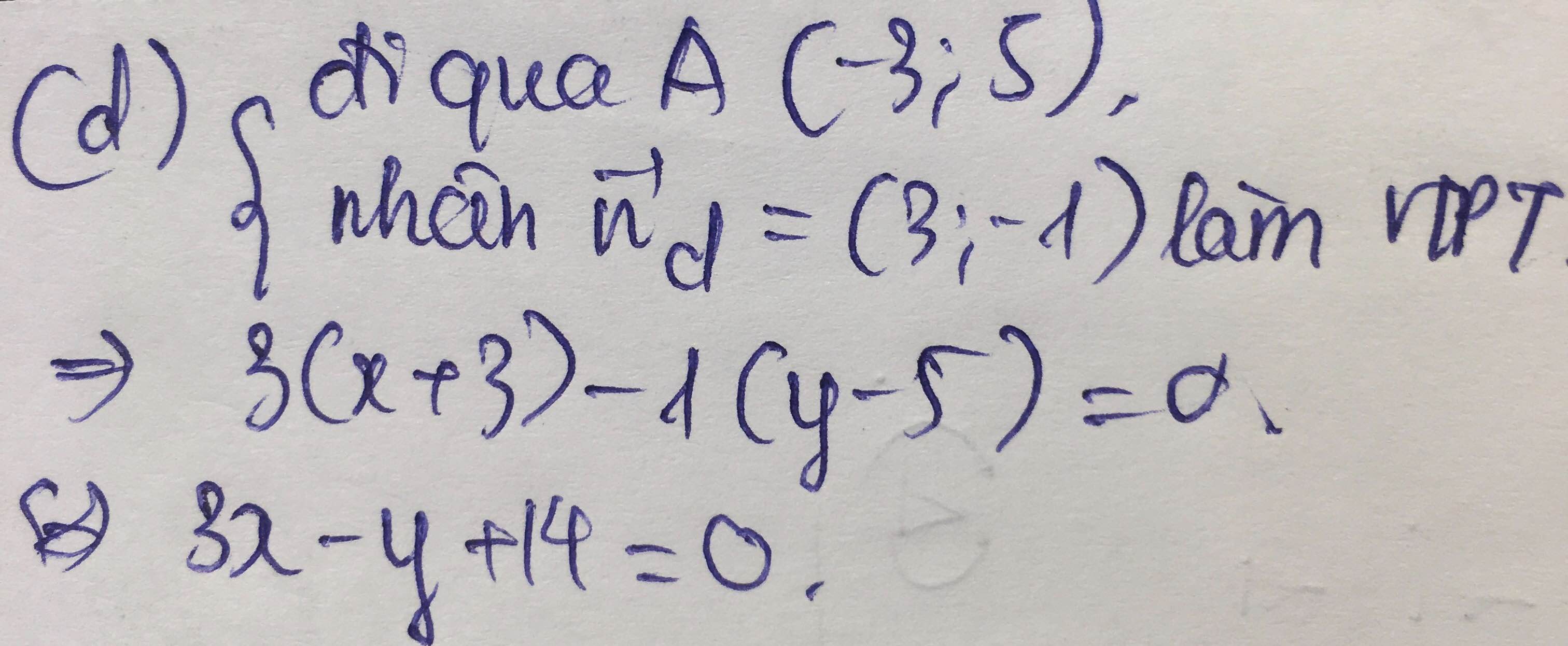
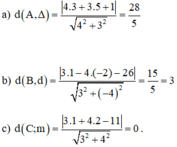
Đáp án D