Cho tam giác ABC, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA
a) Chứng minh AB // CD và AB = CD; AC // BD và AC = BD
b) Gọi E và F lần lượt là trung điểm của AC và BD; AF cắt BC tại I, DE cắt BC tại K Chứng minh: BI = IK = KC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 1 2022
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
23 tháng 4 2023
a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//CD
c: Xét tứ giác ABCE có
N là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//EC
=>C,E,D thẳng hàng
28 tháng 8 2021
a: Xét tứ giác ABDC có
M là trung điểm của đường chéo AD
M là trung điểm của đường chéo BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD và AB=CD
CM
23 tháng 6 2018
a. Hình vẽ (0.5 điểm)
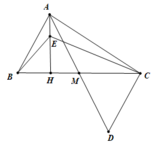
Xét ΔABM và ΔDCM có:
BM = MC
∠(AMB) = ∠(BMC)
AM = MD
⇒ ΔABM = ΔDCM (c.g.c) (0.5 điểm)
⇒ AB = DC (hai cạnh tương ứng) (0.5 điểm)
8 tháng 3 2022
a, Xét tam giác AMB và tam giác DMC có
AM = DM ; BM = MC ; ^AMB = ^DMC (đ.đ)
Vậy tam giác AMB = tam giác DMC (c.g.c)
=> ^ABM = ^DCM ( 2 góc tương ứng )
mà 2 góc này ở vị trí đồng vị
Vậy AB // CD
16 tháng 5 2023
a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//DC
b: Xét ΔKMB và ΔFMC có
góc MBK=góc MCK
MB=MC
góc KMB=góc FMC
=>ΔKMB=ΔFMC
=>MK=MF
=>M là trung điểm của KF
HT
6 tháng 5 2016
K là giao điểm của 3 đường trung tuyến. CN là đường trung tuyến kẻ từ C nên AN=BN
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )
có hình ko vậy ạ