Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

vẽ hình lỗi nên ko vẽ được
a) xét \(\Delta BAM\)VÀ\(\Delta CDM\)CÓ
AM=MD(GT)
\(\widehat{BMA}=\widehat{CMD}\left(Đ^2\right)\)
BM=CM (GT)
=>\(\Delta BAM\)=\(\Delta CDM\)(C-G-C)
=> ab=cd( hai cạnh tương ứng )
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\)HAY\(\widehat{ABC}=\widehat{DCB}\)( hai góc trương ứng)
MÀ HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG = NHAU
\(\Rightarrow AB//CD\left(đpcm\right)\)
xét \(\Delta BDM\)VÀ\(\Delta CAM\)CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{BMD}=\widehat{CMA}\left(Đ^2\right)\)
\(DM=AM\left(GT\right)\)
=>\(\Delta BDM\)=\(\Delta CAM\)(C-G-C)
=> BD=AC ( HAI CẠNH TƯƠNG ỨNG )
\(\Rightarrow\widehat{MBD}=\widehat{MCA}\)HAY\(\widehat{CBD}=\widehat{BCA}\)( HAI GÓC TƯƠNG ỨNG )
HAI GÓC NÀY Ở VỊ TRÍ S SOLE TRONG BẰNG NHAU
=>AC//BD
B) đề sai

Bạn tự vẽ hình nha![]()
a.
Xét tam giác ABO và tam giác CDO có:
AO = CO (BO là trung truyến của tam giác ABC)
AOB = COD (2 góc đối đỉnh)
BO = DO (gt)
=> Tam giác ABO = Tam giác CDO (c.g.c)
=> BAO = DCO (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AB // CD.
b.
BO là trung tuyến của tam giác ABC
=> O là trung điểm của AC
=> AO = CO = \(\frac{1}{2}AC\) (1)
- BO = DO (gt) => CO là trung tuyến của tam giác BCD
- BM = CM (M là trung điểm của BC) => DM là trung tuyến của tam giác BCD
=> I là giao điểm của 2 đường trung tuyến CO và DM của tam giác BCD
=> I là trọng tâm của tam giác BCD.
=> IO = \(\frac{1}{3}OC\) (2)
Thay (1) vào (2), ta có:
IO = \(\frac{1}{3}OC=\frac{1}{3}\times\frac{1}{2}AC=\frac{1}{6}AC\)
\(\Rightarrow AC=6\times IO\)
c.
AB // CD
=> EBM = DCM (2 góc so le trong)
Xét tam giác EBM và tam giác DCM có:
EBM = DCM (chứng minh trên)
BM = CM (M là trung điểm của BC)
BME = CMD (2 góc đối đỉnh)
=> Tam giác EBM = Tam giác DCM (g.c.g)
=> BE = CD (2 cạnh tương ứng)
mà CD = AB (tam giác ABO = tam giác CDO)
=> BE = AB.
Chúc bạn học tốt![]()

a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//DC
b: Xét ΔKMB và ΔFMC có
góc MBK=góc MCK
MB=MC
góc KMB=góc FMC
=>ΔKMB=ΔFMC
=>MK=MF
=>M là trung điểm của KF

a, xét t.giác AMB và t.giác DMC có:
AM=DM(gt)
\(\widehat{AMB}\)=\(\widehat{DMC}\)(vì đối đỉnh)
CM=BM(gt)
=>t.giác AMB=t.giác DMC(c.g.c)
b,đề bài bị thiếu


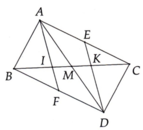

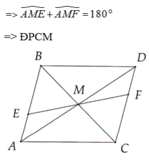
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )
có hình ko vậy ạ