LN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TA
9 tháng 6 2021
TXĐ: `D=RR`
`y'=x^3-4x`
`y'=0 <=>` \(\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
\(\begin{array}{|l|cr|} \hline x & -\infty & & -2 &&&& & 0 & &&&&2&&& & +\infty\\ \hline y' & &-& 0& & &+& &0& &&-&&0& &&+&\\ \hline\end{array}\)
Vậy hàm số đồng biến trên các khoảng: `(-2;0)` và `(2; +\infty)`
Hàm số nghịch biến trên các khoảng: `(-\infty; -2)` và `(0;2)`.
PT
1
CM
11 tháng 5 2017
Đáp án B.
Tập xác định D = R.
y' = 4x3 + 4x
y’ = 0 <=> 4x3 + 4x = 0 <=> x = 0.
Bảng biến thiên
LN
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
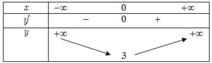
a. ĐKXĐ: \(-3\le x\le3\)
\(y'=1-\dfrac{x}{\sqrt{9-x^2}}=\dfrac{\sqrt{9-x^2}-x}{\sqrt{9-x^2}}=0\Rightarrow x=\dfrac{3\sqrt{2}}{2}\)
Dấu của y':
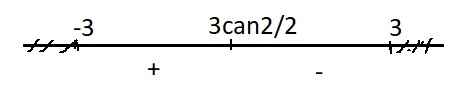
Hàm đồng biến trên \(\left(-3;\dfrac{3\sqrt{2}}{2}\right)\) và nghịch biến trên \(\left(\dfrac{3\sqrt{2}}{2};3\right)\)
b.
ĐKXĐ: \(x\ne2\)
\(y'=\dfrac{\left(-2x-1\right)\left(x+2\right)+x^2+x+2}{\left(x+2\right)^2}=\dfrac{-x^2-4x}{\left(x+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Dấu của y':
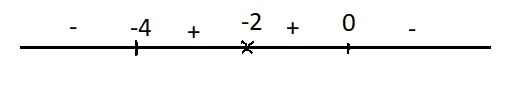
Hàm đồng biến trên các khoảng \(\left(-4;-2\right)\) và \(\left(-2;0\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-4\right)\) và \(\left(0;+\infty\right)\)
CM
23 tháng 3 2018
a)Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:
Quy tắc 1:
1. Tìm tập xác định.
2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
1. Tìm tập xác định.
2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu xi (i = 1, 2, 3, ...) là các nghiệm của nó.
3. Tính f"(x) và f"(xi)
4. Nếu f"(xi) > 0 thì xi là điểm cực tiểu.
Nếu f"(xi) < 0 thì xi là điểm cực đại.
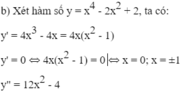
Dựa vào Quy tắc 2, ta có:
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.
y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.
TN
1
HN
20 tháng 10 2021
Tập xác định: D=\(\left[-2\sqrt{2};2\sqrt{2}\right]\).
\(y'=1-\dfrac{x}{\sqrt{8-x^2}}\) = 0 \(\Rightarrow\) x=2.
Bảng biến thiên:
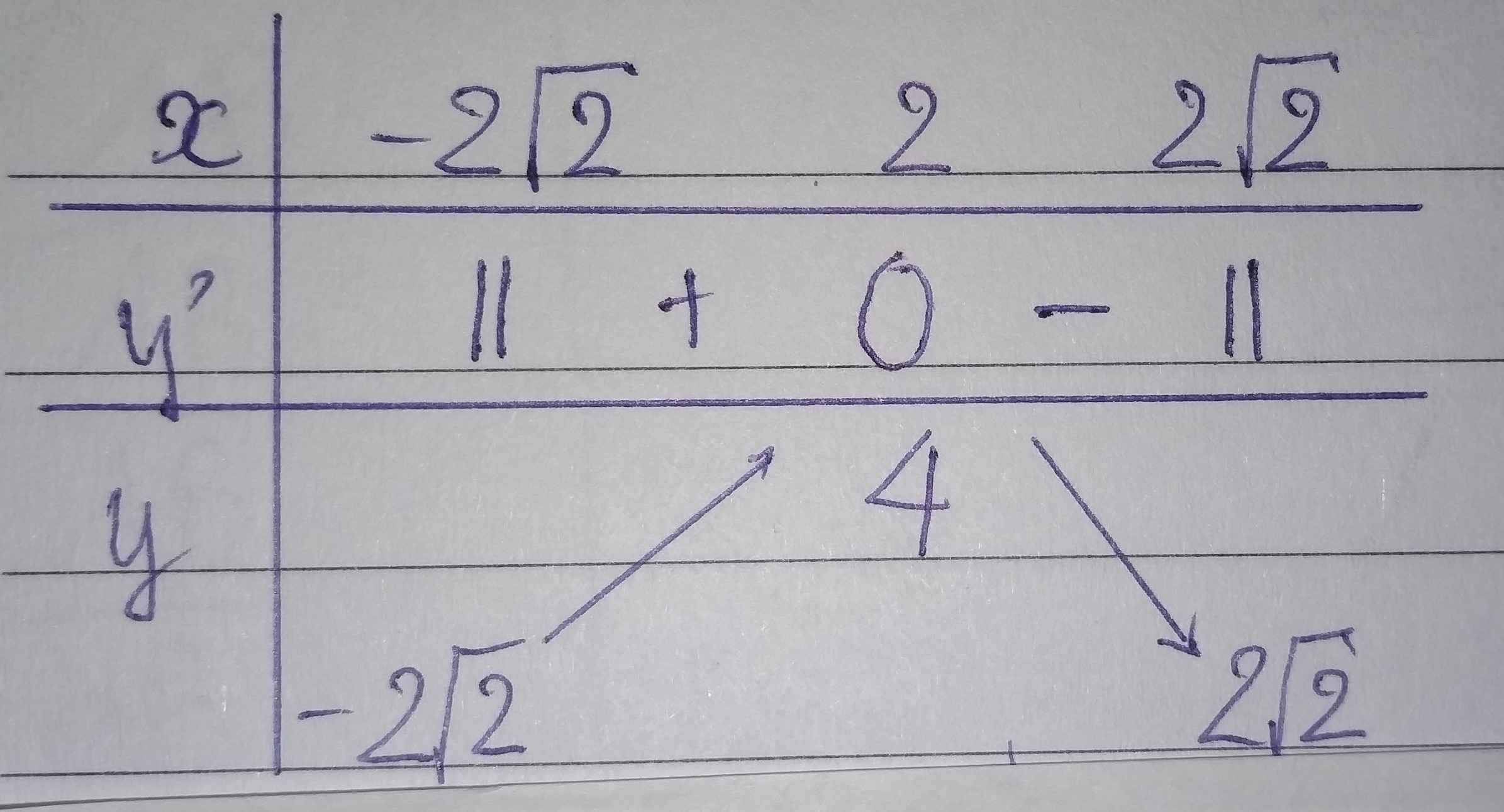
Vậy hàm số đã cho đồng biến trên khoảng (\(-2\sqrt{2}\);2), nghịch biến trên khoảng (2;\(2\sqrt{2}\)) và yCĐ=4 (tại x=2).
Tham khảo: Đồ thị:
CM
21 tháng 2 2017
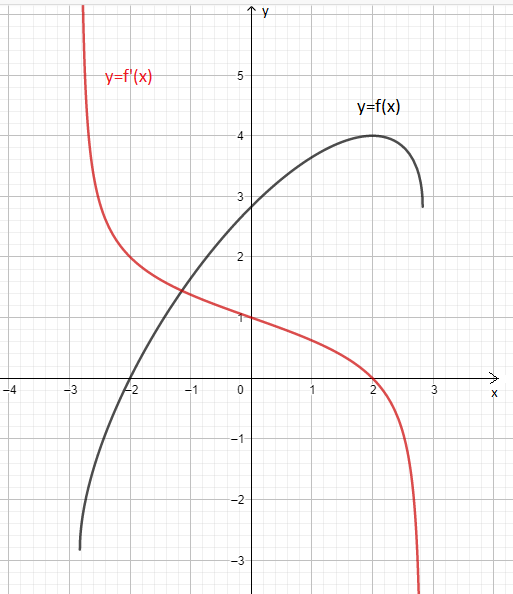
Đáp án A
Phương pháp:
+) Tính y’ và giải phương trình y' = 0
+) Lập bảng xét dấu của y’ và rút ra kết luận.
+) Điểm x = x0 được gọi là điểm cực tiểu của hàm số khi và chỉ khi qua điểm đó y’ đổi dấu từ âm sang dương.
Cách giải:
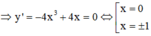
Bảng xét dấu y’:
Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu yCT = y(0) = 2
PT
1
PT
1
CM
10 tháng 1 2019
Chọn A
Ta có: y =
x
4
-
2
x
2
+
3
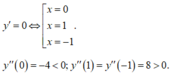
Vậy hàm số đạt cực tiểu tại x = 1; x = -1 và giá trị cực tiểu của hàm số là 
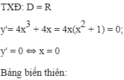
\(y'=-4x^3-4x=-4x\left(x^2+1\right)=0\Rightarrow x=0\)
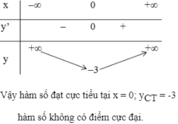
Dấu của y':
Hàm đồng biến trên \(\left(-\infty;0\right)\) và nghịch biến trên \(\left(0;+\infty\right)\)
Qua \(x=0\) ta thấy y' đổi dấu từ dương sang âm nên \(x=0\) là điểm cực đại