Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) chia 12 ghế thành 2 ô, nam ở một ô, nữ ở 1 ô. do vậy có 2 cách sắp xếp cho nam và nữ
sắp xếp các bạn nam ngồi vào ghế có chỉnh hợp chập 6 của 6 cách
tương tự, các bạn nữ cũng có chỉnh hợp chập 6 của 6 cách
như vậy có 2 nhân chỉnh hợp chập 6 của 6 nhân chỉnh hợp chập 6 của 6 bằng 1036800
chắc vậy. Bạn hỏi bọn 11 sẽ ổn hơn

Lời giải:
Số học sinh học ít nhất 1 môn toán là:
$36+16=52$ (hs)
Xác suất để sinh viên học ít nhất 1 môn toán: $\frac{52}{60}$

Kí hiệu tắt ông là M và bà là W. Không gian mẫu E có \(6!=720\) (phần tử).
1.
Có 2 cách xếp người cùng phái ngồi gần nhau: \(MMMWWW,WWWMMM\).
Có \(3!=6\) cách ngồi của 3 ông và có \(3!=6\) cách ngồi của 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
2.
Có 4 cách sắp xếp 3 bà ngồi gần nhau: \(MMMWWW,MMWWWM,MWWWMM,WWWMMM\).
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{4.3!.3!}{6!}=\dfrac{1}{5}\).
3.
Có 2 cách sắp xếp 3 ông và 3 bà ngồi xen kẽ nhau: \(MWMWMW,WMWMWM.\)
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)

Đáp án A
Không gian mẫu là “Chọn ngẫu nhiên 2 người từ 10 học sinh trong tổ đó”. Suy ra số phần tử trong không gian mẫu là n ( Ω ) = C 10 2
Gọi A là biến cố “2 người được chọn là nữ” thì kết quả thuận lợi cho biến cố A là n ( A ) = C 3 2
Vậy xác suất cần tính là P ( A ) = n ( A ) n ( Ω ) = C 3 2 C 10 2 = 1 15 .
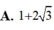
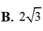
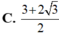
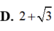

a) Xác suất là 2/10 hoặc 1/5.
b) Xác suất là 3/10 hoặc 3/10. Giải bằng công thức hoặc bảng xác suất.