Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương
a
→
= (3; 3; 1) là: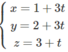 
Phương trình chính tắc của ∆ là:
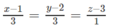
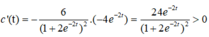
với mọi t ≥ 0 nên c(t) tăng trên [0; +∞] , nghĩa là nồng độ c ngày càng tăng.
Chọn đáp án B.
Chọn C
Do tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc và H là trực tâm tam giác ABC nên 
Phương trình mặt phẳng (ABC) là 
hay 6x + 4y + 3z - 12 = 0
Vì 
nên đường thẳng OH có véc-tơ chỉ phương 
Mà đường thẳng OH đi qua O nên phương trình tham số của đường thẳng OH là: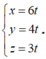 
Chọn D
Phương trinh:
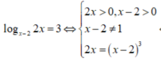
<=> x = 4
Với x=4, thay lần lượt vào các đáp án, ta được log2( x2- 8) =3
a) f' (x)=3x2-6x
f'' (x)=6x-6;f'' (x)=0 < ⇒ x=1 ⇒ f (1) = -1
Vậy I(1; -1)
b) Công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI:
Phương trình của (C) đối với hệ trục IXY là:
y - 1 = (X+1)3-3(X+1)2+1 hay Y=X3-3X
Vì hàm số Y=X3-3X là hàm số lẻ nên đồ thị của nó nhận gốc tọa độ I làm tâm đối xứng.
c) * Tiếp tuyến với (C) tại I(1; -1) đối với hệ tọa độ Oxy là:
y = f' (1)(x-1)+f(1) với f’(1) = -3; f(1) = -1
Nên Phương trình tiếp tuyến: y= -3(x-1)+(-1) hay y = -3x + 2
Xét hiệu (x3-3x2+1)-(-3x+2)=(x-1)3
Với x ∈(-∞;1) ⇒ (x-1)3<0 ⇔ x3 – 3x2 + 1 < -3x +2 nên đường cong (C): y=x3-33+1 nằm phía dưới tiếp tuyến y = -3x + 2
Với x ∈(1; +∞) ⇒ (x-1)3>0 ⇔ x3 – 3x2 + 1 > -3x + 2 nên đường cong (C): nằm phía trên tiếp tuyến tại I.
Chọn D
Giả sử B (5b ; 0 ; 1 + 4b) ∈ BM, C (4 + 16c ; -2-13c ; 3 + 5c) ∈ CH
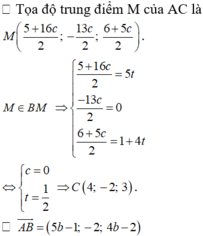
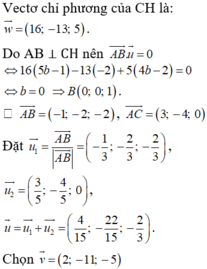
là vectơ chỉ phương của đường phân giác góc A.
Vậy phương trình đường phân giác góc A là: 
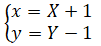
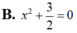
$4Cr + 3O_2 \xrightarrow{t^o} 2Cr_2O_3$
$Cr_2O_3 + 3H_2SO_4 \to Cr_2(SO_4)_3 + 3H_2O$
$Cr_2(SO_4)_3 + 6NaOH \to 2Cr(OH)_3 + 3Na_2SO_4$
$2Cr(OH)_3 \xrightarrow{t^o} Cr_2O_3 + 3H_2O$
$4Cr + 3O_2 \xrightarrow{t^o} 2Cr_2O_3$
$Cr_2O_3 + 3H_2SO_4 \to Cr_2(SO_4)_3 + 3H_2O$
$Cr_2(SO_4)_3 + 6NaOH \to 2Cr(OH)_3 + 3Na_2SO_4$
$2Cr(OH)_3 \xrightarrow{t^o} Cr_2O_3 + 3H_2O$