Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a﴿ Chu vi:
2/5 x 4 = 8/5 ﴾m﴿
Diện tích:
2/5 x 2/5 = 4/25 ﴾m2 ﴿
b﴿ Diện tích 1 ô vuông nhỏ là:
2/25 x 2/25 = 4/625 ﴾m2 ﴿
Số ô vuông cắt được là:
4/25 : 4/625 = 25 ﴾ô vuông﴿
c﴿ Chiều rộng tờ giấy hình chữ nhật là:
4/25 : 4/5 = 1/5 ﴾m﴿

Đáp án B
Gọi O là tâm nửa đường tròn. Ta có: P Q = 2 O P = 2 9 − x 2
Đặt diện tích hình chữ nhật là: f x = 2 x 9 − x 2 ⇒ f 2 x = 4 x 2 9 − x 2
Đặt y = x 2 0 < y ≤ 3 . Xét hàm số g y = 4 y 9 − y
Ta có f x lớn nhất khi g y lớn nhất. g y lớn nhất khi y = 3 ⇒ x = 3
max f x = f 3 = 6 2

Đáp án B
Gọi O là tâm nửa đường tròn. Ta có: P Q = 2 O P = 2 9 − x 2
Đặt diện tích hình chữ nhật là: f x = 2 x 9 − x 2 ⇒ f 2 x = 4 x 2 9 − x 2
Đặt y = x 2 0 < y ≤ 3 . Xét hàm số g y = 4 y 9 − y
Ta có f x lớn nhất khi g y lớn nhất. g y lớn nhất khi y = 3 ⇒ x = 3
max f x = f 3 = 6 2

Đáp án C
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13

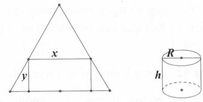
Dựa vào hình vẽ ta suy ra đáy của hình trụ có bán kính là h 2
Theo đề, ta có ![]()
=> h = 4 m
Suy ra kích thước của hình chữ nhật là 12 và 4 π
Diện tích của hình chữ nhật là ![]()
Chọn B.

50% = \(\dfrac{1}{2}\) ⇒ \(\dfrac{1}{2}\) chiều rộng = \(\dfrac{1}{3}\) chiều dài
Tỉ số chiều dài và chiều rộng là: \(\dfrac{1}{3}\):\(\dfrac{1}{2}\) = \(\dfrac{2}{3}\)
a,Nửa chu vi của khu vườn hình chữ nhật là: 200 : 2 = 100
Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có: Chiều rộng khu vườn: 100:(2+3)\(\times\)2 = 40(m)
Chiều dài khu vườn: 100 - 40 = 60(m)
Diện tích khu vườn là: 60 \(\times\)40 = 2400(m2)
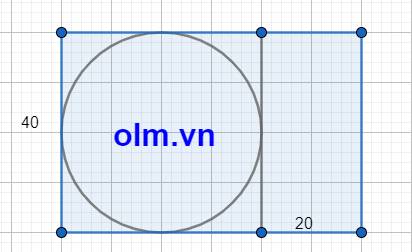
b, Ta chia khu vườn thành hai mảnh trong đó mảnh 1 là hình vuông có cạnh là chiều rộng hình chữ nhật, mảnh còn lại là hình chữ nhật.
Ta sẽ vẽ một hình tròn nội tiếp hình vuông ta sẽ được hình tròn có diện tích lớn nhất có thể và diện tích bằng:
40 \(\times\)40\(\times\) 3,14:4 = 1256 (m2)
Chiều rộng của hình chữ nhật còn lại là: 60 - 40 = 20 (m)
Chiều dài của hình chữ nhật còn lại bằng chiều rông khu vườn và bằng 40 m
Diện tích mảnh đất hình chữ nhật còn lại là: 40 \(\times\) 20 = 800(m2)
Diện tích trồng cây cảnh là: 2400 - 1256 - 800 = 344 (m2)
Đáp số: a, 2400 m2
b, 344 m2

Đáp án A
Phương pháp:
Tính độ dài các đoạn thẳng MN và MQ sau đó áp dụng công thức tình thể tích hình trụ V = π r 2 h

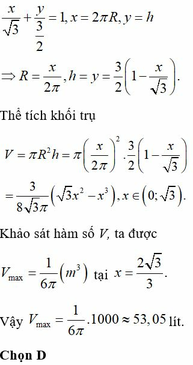

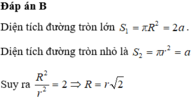
Đáp án B
Hình chữ nhật luôn nội tiếp trên một đường tròn, nên hình chữ nhật lớn nhất có thể cắt ra nội tiếp trên đường tròn bán kính 5cm. Xét hình chữ nhật ABCD bất kỳ nội tiếp (0;5cm) ta có
S A B C D = A B . B C ≤ A B 2 + B C 2 2 = A C 2 2 = 10 2 2 = 50 c m 2