Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
Qua O kẻ đường thẳng vuông góc với MN, đường thẳng này cắt MN, PQ, cung AB,AQ lần lượt tại H,F,D,E
Độ dài cung AB là chu vi đường tròn đáy của hình nón nên
l A B = 2 πr = 2 π . 2 3 = 4 π 3
Lại có l a b = α . O A ⇒ α = l a b O A = 4 π 3 : 2 = 2 π 3 = A O B ⏜
Áp dụng định lý cosin trong tam giác OAB có
A B = O A 2 + O B 2 - 2 . O A . O B . cos A O B ⏜ = 2 2 + 2 2 - 2 . 2 2 - 1 2 = 2 3
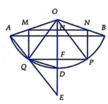Do M,N lần lượt là trung điểm của OA,OB nên
A
O
B
⏜
⇒
A
O
D
⏜
=
60
°
⇒ M H = 1 2 M N = 3 2
Do O D ⊥ A B nên OD là tia phân giác của A O B ⏜ ⇒ A O D ⏜ = 60 ° . Xét tam giác vuông OMH có O H = O M . cos 60 = 1 . 1 2 = 1 2
Xét tam giác OPQ có cos P O Q ⏜ = O P 2 + O Q 2 - P Q 2 2 . O P . O Q = 2 2 + 2 2 - 3 2 2 . 2 . 2 = 5 8
Mà cos P O Q ⏜ = cos 2 D O Q ⏜ = 2 cos 2 D O Q ⏜ - 1 = 5 8 ⇒ cos D O Q ⏜ = 13 4
Xét tam giác DOQ có:
Q D 2 + O Q 2 + O D 2 - 2 . O Q . O D . cos D O Q ⏜ = 8 - 2 13
Xét tam giác vuông DQF có
D F 2 = Q D 2 - Q F 2 = 8 - 2 13 - 3 2 2 = 29 4 - 2 13
⇒ D F = 29 - 8 13 2 = 4 - 13 2 2 = 4 - 13 2
⇒ H F = O D - O H - D F = 2 - 1 2 - 4 - 13 2 = 13 - 1 2 = M Q - N P
Gọi R là bán kính đáy của hình trụ tạo bởi hình chữ nhật MNPQ. Chu vi đáy của hình trụ chính là độ dài của PQ nên P Q = 2 πR → R = 3 2 π
Khi đó thể tích khối trụ tạo ra bởi hình chữ nhật MNPQ là:
V = πR 2 . MQ = π 3 2 π 2 . 13 - 1 2 = 3 13 - 1 8 π
Đáp án A
Phương pháp: Độ dài đường sinh của hình nón 
, trong đó r; h lần lượt là bán kính đáy và chiều cao của hình nón.
Cách giải:
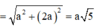
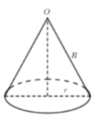
Diện tích hình tròn S = πR 2
Gọi bán kính đường tròn đáy hình nón là r(0<r<R) ta có
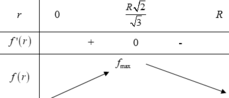
Xét hàm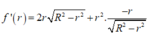 
có 
Bảng biến thiên:
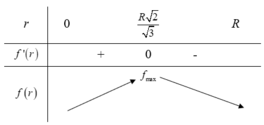
Do đó thể tích V đạt GTLN tại
r
=
R
2
3
. Khi đó
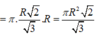
Vậy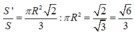 
Chọn đáp án D.
Đáp án D
Phương pháp:
- Lập hàm tinh thể tích khối nón, xét hàm suy ra GTLN.
- Tính diện tích S , S ' với chú ý S là diện tích hình tròn và S ' là diện tích xung quanh của hình nón.
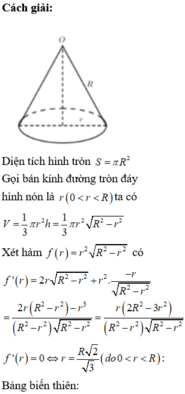
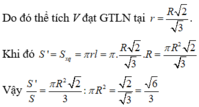
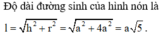
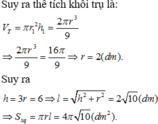
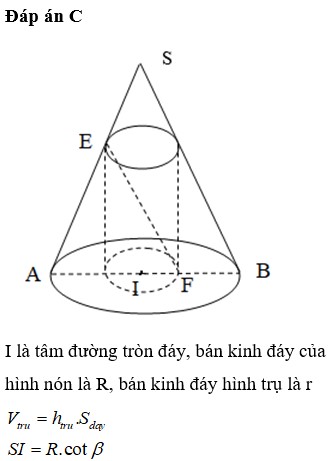
Đáp án A
Phương pháp:
Tính độ dài các đoạn thẳng MN và MQ sau đó áp dụng công thức tình thể tích hình trụ V = π r 2 h