Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
2: Xét ΔIBF và ΔIAB có
góc IBF=góc IAB
góc BIF chung
=>ΔIBF đồng dạng với ΔIAB
=>IB/IA=IF/IB
=>IB^2=IA*IF

Từ một điểm M ở bên ngoài đường tròn tâm O, vẽ hai tiếp tuyến MA, MB với đường tròn (O)( A, B là các tiếp điểm). Gọi E là trung điểm của đoạn thẳng MA, tia EB cắt đường tròn (O) tại C. Tia MC cắt đường tròn (O) tại điểm thứ hai là D. Chứng minh rằng:
a. Tứ giác MAOB nội tiếp;
b. EA2 = EC.EB;
c. BD // MA.

Bạn tự vẽ hình nha
a)Xét tứ giác MAOB có:
\(\widehat{MAO}\)=90'(vì MA là tiếp tuyến của (O))
\(\widehat{MBO}\)=90'(vì MB là tiếp tuyến của (O))
Suy ra \(\widehat{MAO}\)+\(\widehat{MBO}\)=90'+90'=180'
Vậy tứ giác MAOB nội tiếp
b)Xét tam giác ABM có:
MA=MB(tính chất hai tiếp tuyến cắt nhau)
Do đó tam giác MAB là tam giác cân tại M
c)Xét tam giác IBF và IAB có:
\(\widehat{BIA}\)là góc chung
\(\widehat{IBF}\)=\(\widehat{IAB}\)(cùng bằng 1/2 sđ\(\widebat{BF}\))
Do đó tam giác IBF đồng dạng với IAB
Suy ra \(\frac{IB}{IF}=\frac{IA}{IB}\)
<=>\(IB^2=IA.IF\)

Bạn xem lại đề giúp mình nha, vì đề ko có dữ kiện nào liên quan tới điểm C,D hết

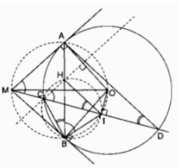

A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.


a)
MA và MB là các tiếp tuyến của (O)
=> OM _I_ AB mà C thuộc OM
=> AC = BC
OB = OA = OC = OD ( = R)
=> \(\Delta ACD\) vuông tại A và \(\Delta BCD\) vuông tại B
\(\Rightarrow\Delta ACD=\Delta BCD\left(ch-cgv\right)\)
\(\Rightarrow\Delta ACD~\Delta BCD\)
\(\Rightarrow\frac{AC}{BC}=\frac{AD}{BD}\)
\(\Rightarrow AC\times BD=AD\times BC\left(\text{đ}pcm\right)\)
b)
AI là đpg của \(\Delta ACD\)
\(\Rightarrow\frac{IC}{ID}=\frac{AC}{AD}\) mà \(\frac{AC}{AD}=\frac{BC}{BD}\)
\(\Rightarrow\frac{IC}{ID}=\frac{BC}{BD}\)
=> BI là đpg của \(\Delta BCD\) (đpcm)
a) MA và MB là các tiếp tuyến của (O)
=> OM _I_ AB mà C thuộc OM
=> AC = BC
OB = OA = OC = OD ( = R)
=> \Delta ACDΔACD vuông tại A và \Delta BCDΔBCD vuông tại B
\Rightarrow\Delta ACD=\Delta BCD\left(ch-cgv\right)⇒ΔACD=ΔBCD(ch−cgv)
\Rightarrow\Delta ACD~\Delta BCD⇒ΔACD ΔBCD
\Rightarrow\frac{AC}{BC}=\frac{AD}{BD}⇒BCAC=BDAD
\Rightarrow AC\times BD=AD\times BC\left(\text{đ}pcm\right)⇒AC×BD=AD×BC(đpcm)
b)
AI là đpg của \Delta ACDΔACD
\Rightarrow\frac{IC}{ID}=\frac{AC}{AD}⇒IDIC=ADAC mà \frac{AC}{AD}=\frac{BC}{BD}ADAC=BDBC
\Rightarrow\frac{IC}{ID}=\frac{BC}{BD}⇒IDIC=BDBC
=> BI là đpg của \Delta BCDΔBCD (đpcm)
giúp với câu b)
b, tam giác MCB ~ tam giác MBA (g.g) => BC/BA =MC/MD (vì MB=MD <= t/c 2 tiếp tuyến cắt nhau) (1)
tam giác MCD ~ tam giác MDA (g.g) => MC/MD= DC/AD (2)
Từ (1),(2) => BC/BA = DC/AD => BC.AD = DC.AB (đpcm)