Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a)Xét tứ giác MAOB có:
\(\widehat{MAO}\)=90'(vì MA là tiếp tuyến của (O))
\(\widehat{MBO}\)=90'(vì MB là tiếp tuyến của (O))
Suy ra \(\widehat{MAO}\)+\(\widehat{MBO}\)=90'+90'=180'
Vậy tứ giác MAOB nội tiếp
b)Xét tam giác ABM có:
MA=MB(tính chất hai tiếp tuyến cắt nhau)
Do đó tam giác MAB là tam giác cân tại M
c)Xét tam giác IBF và IAB có:
\(\widehat{BIA}\)là góc chung
\(\widehat{IBF}\)=\(\widehat{IAB}\)(cùng bằng 1/2 sđ\(\widebat{BF}\))
Do đó tam giác IBF đồng dạng với IAB
Suy ra \(\frac{IB}{IF}=\frac{IA}{IB}\)
<=>\(IB^2=IA.IF\)

Bạn xem lại đề giúp mình nha, vì đề ko có dữ kiện nào liên quan tới điểm C,D hết

1: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
2: Xét ΔIBF và ΔIAB có
góc IBF=góc IAB
góc BIF chung
=>ΔIBF đồng dạng với ΔIAB
=>IB/IA=IF/IB
=>IB^2=IA*IF

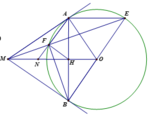
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn
Vẽ được các yếu tố để chứng minh phần (1).
Ta có M B O ^ = 90 0 , M A O ^ = 90 0 (theo t/c của tiếp tuyến và bán kính)
Suy ra: M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF. NA và MN = NH
Ta có A E / / M O ⇒ A E M ^ = E M N ^ mà A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^
Δ N M F v à Δ N A M có: M N A ^ chung; E M N ^ = M A F ^
nên Δ N M F đồng dạng với Δ N A M
⇒ N M N F = N A N M ⇒ N M 2 = N F . N A 1
Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N ^ h a y H B F ^ = F M H ^
=> MFHB là tứ giác nội tiếp
⇒ F H M ^ = F B M ^ = F A B ^ h a y F H N ^ = N A H ^
Xét Δ N H F & Δ N A H c ó A N H ^ c h u n g ; N H F ^ = N A H ^
=> Δ N M F đồng dạng Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A 2
Từ (1) và (2) ta có NH = HM
3) Chứng minh: H B 2 H F 2 − EF M F = 1 .
Xét Δ M AF và Δ M E A có: A M E ^ chung, M A F ^ = M E A ^
suy ra Δ M AF đồng dạng với Δ M E A
⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2 (3)
Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^ = B F H ^
Δ A E F và Δ H B F có: E F A ^ = B F H ^ ; F E A ^ = F B A ^
suy ra Δ A E F ~ Δ H B F
⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2 (4)
Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1
Từ một điểm M ở bên ngoài đường tròn tâm O, vẽ hai tiếp tuyến MA, MB với đường tròn (O)( A, B là các tiếp điểm). Gọi E là trung điểm của đoạn thẳng MA, tia EB cắt đường tròn (O) tại C. Tia MC cắt đường tròn (O) tại điểm thứ hai là D. Chứng minh rằng:
a. Tứ giác MAOB nội tiếp;
b. EA2 = EC.EB;
c. BD // MA.