Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một quả bong tennis có dạng hình cầu, người ta đo được chu vi của dường tròn bao quanh quả bóng là 20,41cm. Vậy một đựng bóng tennis cao 19,5cm có thể chứa nhiều nhất bao nhiêu quả bóng ten-nít? lớp 5 help tui

| Loại bóng | Quả bóng gôn | Quả khúc côn cầu | Quả ten-nit | Quả bóng bàn | Quả bi-a |
| Đường kính | 42,7mm | 7,32cm | 6,5cm | 40mm | 61mm |
| Độ dài đường tròn lớn | 134,08mm | 23cm | 20,41cm | 125,6mm | 171,71mm |
| Diện tích | 57,25cm2 | 168,25cm2 | 132,67cm2 | 5024mm2 | 11683,94mm2 |
| Thể tích | 40,74cm3 | 205,26cm3 | 143,72cm3 | 33,49 cm3 | 118,79cm3 |
Cách tính:
+ Quả bóng gôn:
d = 42,7mm ⇒ R = d/2 = 21,35 mm
⇒ Độ dài đường tròn lớn: C = 2π.R=2.3,14.21,35 ≈ 134,08 (mm)
⇒ Diện tích mặt cầu: S = πd2 = 3,14.(42,7)2 ≈ 5725 mm2 = 57,25 (cm2).
⇒ Thể tích khối cầu: 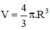
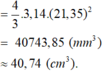
+ Quả khúc côn cầu:
C = πd = 23cm ⇒ 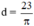 ≈ 7,32 (cm)
≈ 7,32 (cm)
⇒ Diện tích mặt cầu: S = πd2=3,14.(7,32)2 = 168,25 (cm2).
⇒ Thể tích khối cầu: 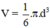
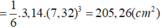
+ Quả ten-nít:
d = 6,5cm
⇒ Độ dài đường tròn lớn: C = π.d = 3,14.6,5 = 20,41 (cm)
⇒ Diện tích mặt cầu: S = πd2= 3,14.(6,5)2=132,67 (cm2)
⇒ Thể tích khối cầu: 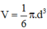
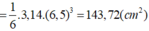
+ Quả bóng bàn:
d = 40mm
⇒ Độ dài đường tròn lớn C = π.d =3,14.40 ≈ 125,6 (mm)
⇒ Diện tích mặt cầu: S = π.d2=3,14.402 = 5024 (mm2)
⇒ Thể tích khối cầu: 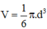
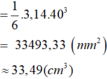
+ Quả bi-a;
d = 61mm
⇒ Độ dài đường tròn lớn C = π.d =3,14.61 = 191,54 (mm)
⇒ Diện tích mặt cầu: S = π.d2=3,14.612 ≈ 11683,94 (mm2)
⇒ Thể tích khối cầu: 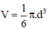
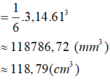

Từ công thức \(S_{cầu}=4\pi r^2=1256\left(cm^2\right)\)
\(\Rightarrow r^2=\dfrac{1256}{4\pi}\approx100\left(cm\right)\Rightarrow r\approx10\left(cm\right)\)

Sửa đề: Chu vi là 69,08cm
Độ dài bán kính là 69,08:2:3,14=11(cm)
Sxq=11^2*4*3,14=1519,76cm2
V=4/3*pi*11^3=5572,45cm3

bn cho mình gửi sắp đến thi học kì 2 rồi. đây là những món quà mà bn sẽ nhận đc:
1: áo quần
2: tiền
3: đc nhiều người yêu quý
4: may mắn cả
5: luôn vui vẻ trong cuộc sống
6: đc crush thích thầm
7: học giỏi
8: trở nên xinh đẹp
phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người, sau 3 ngày bn sẽ có những đc điều đó. nếu bn ko gửi tin nhắn này cho 25 người thì bn sẽ luôn gặp xui xẻo, học kì 2 bn sẽ là học sinh yếu và bạn bè xa lánh( lời nguyền sẽ bắt đầu từ khi đọc) ( mình
cũng bị ép);-;
Diện tích bề mặt quả bóng đó là:
\(S=4\pi r^2\approx4.3,14.9,5^2\approx1133,54\left(cm^2\right)\)

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

Xét 2 tập hợp \(A=\left\{1;2;3;....;25000\right\}\) và \(B=\left\{1;3;3\cdot2;3\cdot2^2;.....;3\cdot2^{13}\right\}\)
Mà \(3\cdot2^{13}=24576< 25000\)
\(\Rightarrow B\subset A\)
Do tập B có 15 phần tử, mỗi quả bóng được sơn 1 màu mà có 7 màu nên theo nguyên lý Dirichlet tồn tại 3 quả bóng cùng màu
Giả sử 3 quả bóng đó được đánh số a > b > c thì \(a⋮b;b⋮c\) và \(abc\ge18>17\)
Vậy ta có đpcm
Để tính diện tích bề mặt của quả bóng, ta sử dụng công thức diện tích bề mặt của hình cầu:
Diện tích bề mặt của hình cầu = 4πr^2
Trong đó, r là bán kính của quả bóng. Với đường kính của quả bóng bằng 22 cm, ta có bán kính r = 22 cm / 2 = 11 cm.
Thay giá trị của r vào công thức, ta có:
Diện tích bề mặt của quả bóng = 4π(11 cm)^2
Diện tích bề mặt của quả bóng = 4π(121 cm^2)
Diện tích bề mặt của quả bóng ≈ 1520.53 cm^2
Vậy diện tích bề mặt của quả bóng là khoảng 1520.53 cm^2.
câu này là trong đề thi tỉnh Kiên Giang mới thi hôm qua, tui làm ra 484π nhưng khi coi đáp án thì lại là 121π nên tui mới nhờ mn xem dùm