Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khoảng cách giữa 2 đáy trụ là : \(5.6,4=32\left(cm\right)\)
- Bán kính hình trụ đó là : \(6,4:2=3,2\left(cm\right)\)
-> \(S_{xungquanh}=2\pi.r.h=2\pi.32.3,2=\frac{1024\pi}{5}\left(cm^2\right)\)

Một quả bong tennis có dạng hình cầu, người ta đo được chu vi của dường tròn bao quanh quả bóng là 20,41cm. Vậy một đựng bóng tennis cao 19,5cm có thể chứa nhiều nhất bao nhiêu quả bóng ten-nít? lớp 5 help tui

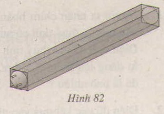
Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::
S Xq = 4 . 4 . 120 = 1920 cm 2
Kiến thức áp dụng
Diện tích xung quanh của hình hộp chữ nhật: Sxq = 2(a + b).h
với a, b là độ dài hai cạnh của hình chữ nhật, h là chiều cao của hình chữ nhật.

Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::
Sxq= 4.4.120 = 1920 cm2

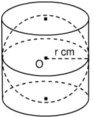
a) Hình cầu bán kính r, vậy thể tích của nó là 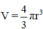
b) Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: V 1 = π r 2 ⋅ 2 r = 2 π r 3
c) Thể tích hình trụ trừ đi thể tích hình cầu là:
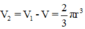
d) Thể tích hình nón có bán kính đáy r, chiều cao 2r
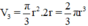
e) Từ các kết quả trên suy ra: Thể tích hình nón "nội tiếp" trong một hình trụ thì bằng thể tích hình trụ trừ đi thể tích hình cầu nội tiếp trong hình trụ ấy.
Hoặc: Thể tích hình trụ bằng tổng thể tích hình nón và hình cầu nội tiếp hình trụ.

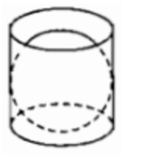
Hình cầu đặt khít trong hình trụ nên bán kính hình cầu bằng bán kính đáy hình trụ, chiều cao hình trụ bằng đường kính hình cầu
Thể tích hình trụ: V 1 = π . r 2 .h = π r 2 .2r = 2 π r 3
Thể tích hình cầu: V 2 = (4/3.) π r 3
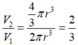
Chọn (D) 2/3

Diện tích xung quanh hình trụ bằng 314 c m 2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2 π r 2 = 31 ⇒ r 2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π ⋅ r 2 h = π ⋅ r 3 ≈ 1109 , 65 cm 3
Kiến thức áp dụng
Hình trụ có bán kính đáy r, chiều cao h thì:
+ Diện tích xung quanh: Sxq = 2πrh
+ Thể tích: V = π.r2.h


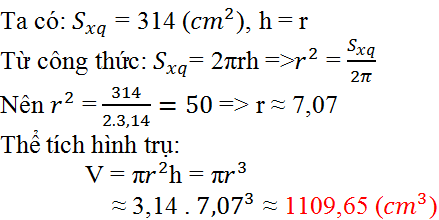
Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3