Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Giả sử theo kế hoạch mỗi ngày người đó dự định may $a$ khẩu trang.
ĐK: $a\in\mathbb{N}^*$
Thời gian dự định: $\frac{1000}{a}$ (ngày)
Thực tế:
Mỗi ngày người đó may: $a+30$ (khẩu trang)
Số ngày may: $\frac{1000}{a}-1$ (ngày)
Số khẩu trang thực tế:
$(a+30)(\frac{1000}{a}-1)=1000+170$
$\Leftrightarrow a^2+200a-30000=0$
$\Rightarrow a=100$
Vậy mỗi ngày người đó dự định may 100 khẩu trang.

Lời giải:
Giả sử theo dự định mỗi giờ tổ sản xuất làm $a$ khẩu trang và làm trong $b$ giờ
Theo bài ra ta có:
$b=\frac{600}{a}$
$b-1=\frac{400}{a}+\frac{200}{a+10}$
$\Rightarrow 1=\frac{600}{a}-(\frac{400}{a}+\frac{200}{a+10})$
$\Leftrightarrow 1=\frac{200}{a}-\frac{200}{a+10}$
Kết hợp với điều kiện $a>0$ suy ra $a=40$ (chiếc)
Vậy theo dự định mỗi h làm $40$ chiếc khẩu trang.

Gọi năng suất dự định là x (0 < x < 20, sản phẩm/giờ)
Sản phẩm làm được sau 2 giờ là: 2x (sản phẩm)
Số sản phẩm còn lại là 120 – 2x (sản phẩm)
Năng suất sau khi cải tiến là x + 3 (sản phẩm/giờ)
Thời gian làm số sản phẩm còn lại là: 120 - 2 x x + 3 (giờ)
Do sau khi cải tiến người đó hoàn thành kế hoạch sớm hơn dự định 1 giờ 36 phút
Đổi 1 giờ 36 phút bằng 1,6 giờ
Theo bài ra ta có phương trình:
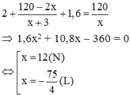
Vậy năng suất dự định của công nhân đó là 12 sản phẩm/giờ
Đáp án C

Gọi số khẩu trang công ti dự định may mỗi ngày là \(x\)(khẩu trang , \(x\in N^∗,x>0\))
số khẩu trang công ti thực tế may mỗi ngày là \(x+100\)(khảu trang)
Thời gian công ti dự dịnh hoàn thành công việc là \(\frac{6000}{x}\)(ngày)
Thời gian công ti thực tế hoàn thành công việc là \(\frac{6000}{x+100}\)(ngày)
Vì thời gian thực tế hoàn thành sớm hơn 2 ngày so với dự định, ta có phương trình:
\(\frac{6000}{x}-\frac{6000}{x+100}=2\)
\(\Leftrightarrow\frac{6000.\left(x+100\right)}{x.\left(x+100\right)}-\frac{6000x}{x.\left(x+100\right)}=\frac{2x.\left(x+100\right)}{x.\left(x+100\right)}\)
\(\Leftrightarrow6000x+600000-6000x=2x^2+200x\)
\(\Leftrightarrow2x^2+200x-600000=0\)
\(\Leftrightarrow x^2+100x-300000=0\)
\(\Leftrightarrow x^2-500x+600x-300000=0\)
\(\Leftrightarrow x.\left(x-500\right)+600.\left(x-500\right)=0\)
\(\Leftrightarrow\left(x-500\right).\left(x+600\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-500=0\\x+600=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=500\left(TM\right)\\x=-600\left(L\right)\end{cases}}}\)
Vậy số khẩu trang công ti dự định may mỗi ngày là \(500\)khẩu trang
Gọi x là khẩu trang cty may đc mỗi ngày theo dự định \(\left(x\inℕ^∗\right)\)
Sau khi bổ sung thêm công nhân thì mỗi ngày may đc: \(x+100\) ( khẩu trang)
Số ngày để may khẩu trang theo dự định là:\(\frac{6000}{x}\)(ngày)
Số ngày để mày khẩu trang khi bổ sung thêm công nhân là:\(\frac{6000}{x+100}\)(ngày)
Vì hoàn thành sớm hơn 2 ngày so với dự định nên ta có pt:
\(\frac{6000}{x}-\frac{6000}{x+100}=2\)
\(\Rightarrow6000\left(x+100\right)-6000x=2x\left(x+100\right)\)
\(\Rightarrow2x^2+200x-600000=0\)
\(\Rightarrow\orbr{\begin{cases}x=500\left(TM\right)\\x=-600\left(L\right)\end{cases}}\)
Vậy dự đinh mỗi ngày cty mày đc 500 chiếc khẩu trang

Gọi x là số giờ làm khẩu trang
Gọi y là số khẩu trang làm trong 1 giờ \(\left(ĐK:x;y>0\right)\)
Theo đề, ta có
\(\hept{\begin{cases}xy=400\\\frac{1}{2}xy+\left(\frac{1}{2}x-1\right)\left(y+100\right)=400\end{cases}}\)
\(\hept{\begin{cases}xy=400\\\frac{1}{2}xy+50x-y-100=200\end{cases}}\)
\(\hept{\begin{cases}xy=400\\50x-y=100\end{cases}}\)
\(\hept{\begin{cases}y=\frac{400}{x}\\50x-\frac{400}{x}=100\end{cases}}\)
\(\hept{\begin{cases}y=\frac{400}{x}\\50x^2-100x-400=0\end{cases}}\)
\(\hept{\begin{cases}y=\frac{400}{x}\\x^2-2x-8=0\end{cases}}\)
\(\hept{\begin{cases}y=\frac{400}{x}\\x=4\left(n\right);x=-2\left(l\right)\end{cases}}\)
\(\hept{\begin{cases}y=100\\x=4\end{cases}}\)

Gọi số khẩu trang mỗi ngày phải may là x
Theo đề, ta có: 300/x-280/(x+10)=3
=>(300x+3000-280x)/(x^2+10x)=3
=>3x^2+30x=20x+3000
=>x=30