Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài: Với bức xạ λ1 thì 10i1 = MN = 20mm → i1 = 2mm.
\(\frac{\iota_1}{\iota_2}=\frac{\text{λ}_1}{\text{λ}_2}=\frac{3}{5}\)\(\rightarrow\iota_2=\frac{10}{3}mm\rightarrow N_2=2.\left[\frac{MN}{2\iota_2}\right]+1=7\)

M, N là hai vân sáng, trên đoạn MN có 10 vân tối => có 11 vân sáng. Tức là có 10 khoảng vân.
\(10i_1 = 20 mm=> i_1 = 2mm.\)
\(\frac{i_1}{i_2}= \frac{\lambda_1}{\lambda_2}= \frac{3}{5}=> i_2 = \frac{10}{3}mm.\)
Nhận xét: \(\frac{MN}{i_2}= 6\)=> có 7 vân sáng.

Giả sử ta dịch vân sáng trung tâm về M thì N là vị trí vân sáng thứ 10(có 10 vân tối)
\(\Rightarrow i_1=2mm\) , Khi thay \(\lambda_1\) bằng \(\lambda_2\) \(\Rightarrow\frac{i_1}{i_2}=\frac{\lambda_1}{\lambda_2}\Rightarrow i_2=\frac{i_1\lambda_2}{\lambda_1}=\frac{10}{3}mm\)
M là vị trí của 1 vân giao thoa,Ta có:
Vân trung tâm trên màn không đổi⇒ta tìm vị trí trùng nhau của 2 loai ánh sáng với 2 khoảng vân khác nhau hay tương ứng với khoảng cách từ vân trung tâm tới M.Ta chia 2 TH như sau:
TH1: M là vân tối
\(\frac{10}{3}.\left(n,5\right)=2k\) với n,k nguyên thì phương trình vô nghiệm
TH2:M là vân sáng
\(\frac{10}{3}.x=2y\)
ới x,y nguyên thì phương trình có nghiệm (3;5) và (6;10)
cả 2 nghiệm này đều kết luận trên MN có 7 vân sáng
----->chọn A

Gọi N là tâm vị trí vân sáng.
\(x_M=20mm\)
MN có 10 vân tối \(\Rightarrow i_1=\dfrac{20}{10}=2mm\)
Ta có: \(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}\Rightarrow\dfrac{2}{i_2}=\dfrac{3}{5}\Rightarrow i_2=\dfrac{10}{3}mm\)
Số vân sáng trên MN lúc này:
\(\dfrac{20}{i_2'}=\dfrac{20}{\dfrac{10}{3}}\Rightarrow i_2'=7\)

Giả sử ta dịch vân sáng trung tâm về M thì N là vị trí vân sáng thứ 10(có 10 vân tối)
\(\Rightarrow i_1=2mm\) ,Khi thay \(\text{λ}_1\)bằng \(\text{λ}_2\)\(\Rightarrow\frac{i_1}{i_2}=\frac{\text{λ}_1}{\text{λ}_2}\Rightarrow i_2=\frac{i_1\text{λ}_2}{\text{λ}_1}=\frac{10}{3}mm\)
M là vị trí của 1 vân giao thoa,Ta có:
Vân trung tâm trên màn không đổi \(\Rightarrow\)ta tìm vị trí trùng nhau của 2 loai ánh sáng với 2 khoảng vân khác nhau hay
tương ứng với khoảng cách từ vân trung tâm tới M.Ta chia 2 TH như sau:
TH1: M là vân tối
\(\frac{10}{3}.\left(n,5\right)=2k\)với n,k nguyên thì phương trình vô nghiệm
TH2:M là vân sáng
\(\frac{10}{3}.x=2y\) với x,y nguyên thì phương trình có nghiệm (3;5) và (6;10)
cả 2 nghiệm này đều kết luận trên MN có 7 vân sáng
-----> chọn A

Khi thực hiện thí nghiệm với bước sóng λ1 thì số khoảng vân là 12, bề rộng trường giao thoa là L = 12i1
Khi thực hiện thí nghiệm với bước sóng λ2, do
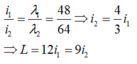
Do M, N là các vân tối nên vân sáng gần M, N nhất cách M, N lần lượt là 0,5i2, suy ra số khoảng vân liên tiếp cho vân sáng là
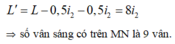
Đáp án D
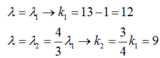
Cách giải: Đáp án D
Ta có
Vậy tại M lúc sau phải là vị trí của vân tối của λ2.Từ kết quả trên ta suy ra: MN = 10i1 =14i2 .Vậy trên đoạn MN có 15 vân tối.