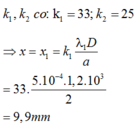Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án A
+ Ta chú ý rằng có (n+1) vân sáng liên tiếp thì cách nhau d = n i
Suy ra, nếu ta xét d = i 123 = n x i x thì có n + 1 vân của bức xạ λ x khoảng ở giữa có n + 1 − 1 − 1 = n − 1 vân (vì không xét 2 vân ở mút)
+ Từ đó ta thiết lập:
i 123 = 12 i 1 = 9 i 2 = 8 i 3 = 3 i 12 = i 23 = 4 i 13
Giải thích lập tỷ số
i 1 i 2 = λ 1 λ 2 = 3 4 ⇒ i 12 = 4 i 1 = 3 i 2 ( 1 ) i 2 i 3 = λ 2 λ 3 = 8 9 ⇒ i 23 = 9 i 2 = 8 i 3 ( 2 ) i 3 i 1 = λ 3 λ 1 = 3 2 ⇒ i 31 = 2 i 3 = 3 i 1 ( 3 ) i 12 i 3 = 4 i 1 3 i 1 / 2 = 8 3 ⇒ i 123 = 3 i 12 = 8 i 3 ( 4 )
Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là N = N 1 + N 2 + N 3 − 2 N 12 + N 23 + N 13 = 11 + 8 + 7 − 2 2 + 0 + 3 = 16

Đáp án C
Điều kiện để hai bức xạ cho vân sáng rùng nhau là
x 1 = x 2 ⇔ k d λ d = k 1 λ 1 ⇔ λ d = k 1 λ 1 k d
Mà 6,4 ≤ λ d ≤ 7,6 → 5,6. k 1 7,6 ≤ k d ≤ 5,6. k 1 6,4
Vì giữa hai vân cùng màu với vân trung tâm có 8 vân màu lục nên k 1 = 9 , thay vào trên ta được k d = 7 vào ta được bước sóng của ánh sáng đỏ là 7,2 μ m

Đáp án C
Khoảng vân: ![]()
Số vân sáng, tối quan sát được trên trường giao thoa:
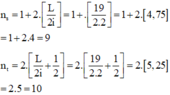

Đáp án A
Ta có: k 1 k 2 = λ 2 λ 1 = 0 , 4 0 , 6 = 2 3 = 2 n 3 n ⇒ k 1 = 2 n
Vị trí vân sáng trùng: x s t = k 1 i 1 = k 2 i 2 ⇒ x s t = 2 n i 1
Số vân sáng trùng trong khoảng giữa 2 vân bậc 7 của λ 1 = λ thỏa điều kiện:
− 7 i 1 < x s t < 7 i 1 ⇔ − 7 i 1 < 2 n i 1 < 7 i 1 ⇔ − 3 , 5 < n < 3 , 5 ⇒

Đáp án A.
- Tại vị trí hai vân sáng trùng nhau:
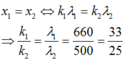
- Vân sáng gần nhất ứng với các số nguyên