Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

uBC(6;0)=>nAH(0,6) ( vì AH vuông góc với BC)
PTTQ của đg thẳng AH đi qua A là
\(0\left(x-3\right)+6\left(y-0\right)=0< =>6y=0\)
b)\(d\left(C;AH\right)=R=\dfrac{\left|6.1\right|}{\sqrt[]{0^2+6^2}}=1\)
PT đg tròn tầm C tiếp xúc AH là
\(\left(x-4\right)^2+\left(y-1\right)^2=1^2\)

a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)

a: vecto BC=(2;7)
=>AH có vtpt là (2;7)
Phương trình AH là:
2(x-2)+7(y-1)=0
=>2x-4+7y-7=0
=>2x+7y-11=0
b: \(IB=\sqrt{\left(3-1\right)^2+\left(1+5\right)^2}=\sqrt{40}\)
Phương trình (C) là:
(x-3)^2+(y-1)^2=40

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
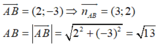
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
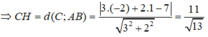
Diện tích tam giác ABC là:
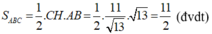
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
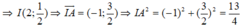
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
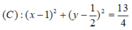

a: vecto BC=(1;-3)
=>VTPT là (3;1)
Phương trình BC là:
3(x-2)+y-2=0
=>3x-6+y-2=0
=>3x+y-8=0
b: Phương trình AH nhận vecto BC làm VTPT
=>Phương trình AH là:
1(x-1)+(-3)*(y-1)=0
=>x-1-3y+3=0
=>x-3y+2=0
c: Tọa độ M là:
\(\left\{{}\begin{matrix}x=\dfrac{1+3}{2}=2\\y=\dfrac{1-1}{2}=0\end{matrix}\right.\)
M(2;0); B(2;2)
vecto BM=(0;-2)
=>VTPT là (2;0)
Phương trình BM là:
2(x-2)+0(y-0)=0
=>2x-4=0
=>x=2