Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần tử của không gian mẫu là n Ω = C 40 3
Gọi A là biến cố: “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là n A = C 10 1 C 10 2 + C 10 2 C 10 1 + C 10 1 C 10 1 C 10 1
Vậy xác suất cần tìm là
P A = n A n C = C 10 1 C 10 2 + C 10 2 C 10 1 + C 10 1 C 10 1 C 10 1 C 40 3 = 120 247
Đáp án A

Đáp án C
Không gian mẫu là cách chọn môn tự chọn và số mã đề thi có thể nhận được của An và Bình.
• An có C 3 2 cách chọn hai môn tự chọn, có C 8 1 . C 8 1 mã đề thi cỏ thể nhận cho 2 môn tự chọn của An.
• Bình giống An. Nên số phần tử của không gian mẫu là n Ω = C 3 2 . C 8 1 . C 8 1 =36864.
Gọi X là biến cổ “ An và Bình có chung đúng một môn thi tự chọn và chung một mã đề”
Số cách chọn môn thi tự chọn của An và Bình là C 3 1 . 2 ! = 6 .
Trong mồi cặp để mà đề cùa An và Bình giống nhau khi An và Bình cùng mã đề của môn chung, với mỗi cặp có cách nhận mã đề cua An và Bình là C 3 2 . C 8 1 . C 8 1 = 512
Do đó, số kết quả thuận lợi của biến cố X là n X = 6 . 512 = 3072 .
Vây xác suât cân tính là P = n X n Ω = 3072 36864 = 1 12 .

A là tập hợp các học sinh thi Khoa học tự nhiên gồm 20 phần tử.
В là tập hợp các học sinh thi Khoa học xã hội gồm 25 phần tử.
A ∩ B là tập hợp các học sinh thi cả hai tổ hợp.
Khi đó: Số học sinh trong lóp bằng: 40 học sinh.
Số cách chọn lần lượt 3 học sinh trong lớp bằng số chỉnh hợp chập 3 của 40 là A 40 3 Chọn A
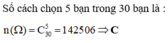
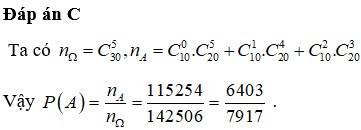




Đáp án B
Gọi A là biến cố “học sinh đăng ký Toán”
Gọi B là biến cố “học sinh đăng ký Lý”
A ∩ B “học sinh đăng ký Toán, Lý”
A ∪ B là biến cố “học sinh có đăng ký học phụ đạo”
P ( A ∪ B ) = P ( A ) + P ( B ) - P ( A ∩ B ) = 38 50 + 30 50 - 25 50 = 43 50
A ∪ B là biến cố “học sinh không đăng ký môn nào cả”
P A ∪ B = 1 - Q A ∪ B = 8 50 = 0 , 14