Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần tử của không gian mẫu là n Ω = C 40 3
Gọi A là biến cố: “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là n A = C 10 1 C 10 2 + C 10 2 C 10 1 + C 10 1 C 10 1 C 10 1
Vậy xác suất cần tìm là
P A = n A n C = C 10 1 C 10 2 + C 10 2 C 10 1 + C 10 1 C 10 1 C 10 1 C 40 3 = 120 247
Đáp án A

Đáp án B
Gọi A là biến cố “học sinh đăng ký Toán”
Gọi B là biến cố “học sinh đăng ký Lý”
A ∩ B “học sinh đăng ký Toán, Lý”
A ∪ B là biến cố “học sinh có đăng ký học phụ đạo”
P ( A ∪ B ) = P ( A ) + P ( B ) - P ( A ∩ B ) = 38 50 + 30 50 - 25 50 = 43 50
A ∪ B là biến cố “học sinh không đăng ký môn nào cả”
P A ∪ B = 1 - Q A ∪ B = 8 50 = 0 , 14

Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu:
n Ω = C 9 3
A: “Số học sinh nam nhiều hơn số học sinh nữ”
Ta có 2 trường hợp:
+) Chọn ra 2 nam, 1 nữ:
+) Chọn ra 3 nam, 0 nữ.
⇒ n A = C 5 2 C 4 1 + C 5 3
⇒ P A = n A n Ω = C 5 2 C 4 1 + C 5 3 C 9 3 = 25 42

Chọn C

Gọi A là biến cố để Hùng và Hương chỉ có chung đúng một môn tự chọn và một mã đề thi. Các cặp gồm 2 môn thi tự chọn mà mỗi cặp có đúng một môn thi là 3 cặp, gồm:
Cặp thứ nhất (Vật lý, Hóa học) và (Vật lý, Sinh học)
Cặp thứ hai ( Hóa học,Vật lý) và (Hóa học, Sinh học)
Cặp thứ ba (Sinh học, Hóa học) và (Sinh học,Vật lý)


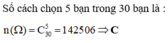
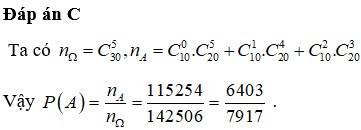
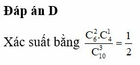


A là tập hợp các học sinh thi Khoa học tự nhiên gồm 20 phần tử.
В là tập hợp các học sinh thi Khoa học xã hội gồm 25 phần tử.
A ∩ B là tập hợp các học sinh thi cả hai tổ hợp.
Khi đó: Số học sinh trong lóp bằng: 40 học sinh.
Số cách chọn lần lượt 3 học sinh trong lớp bằng số chỉnh hợp chập 3 của 40 là A 40 3 Chọn A
câu A