Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
. Mặt phẳng (P): ax + by + cz – 2 = 0 đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T = a + b + c
Chọn A.
Phương pháp:
Cách giải: Tâm mặt cầu là I(-1;1;0) bán kính mặt cầu là R = 2.
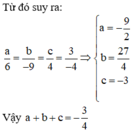
Đáp án B
Gọi J là hình chiếu vuông góc của I lên AB
A B → - 2 ; 2 ; 0 ⇒ A B : x = 1 - t y = t z = 2 J ∈ A B ⇒ J 1 - t ; t ; 2 ⇒ I J → - t ; t - 2 ; - 1 I J → . A B → = 0 ⇔ 2 t + 2 t - 4 = 0 ⇔ t = 1 ⇒ J ( 0 ; 1 ; 2 )
Thiết diện của (P) với (S) có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ I đến (P) lớn nhất khi và chỉ khi d(I;(P))=d(I;(AB)) =IJ
Vậy (P) là mặt phẳng đi qua J và có VTPT I J →
=> (P): x+(y-1)+(z-2)=0 <=> -x-y-z+3=0
=> T=-3
Đáp án B
Gọi J là hình chiếu vuông góc của I lên AB
A B → ( − 2 ; 2 ; 0 ) ⇒ A B : x = 1 − t y = t z = 2 J ∈ A B ⇒ J ( 1 − t ; t ; 2 ) ⇒ IJ → ( − t ; t − 2 ; − 1 ) IJ → . A B → = 0 ⇔ 2 t + 2 t − 4 = 0 ⇔ t = 1 ⇒ J ( 0 ; 1 ; 2 )
Thiết diện của (P) với (S) có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ I đến (P) lớn nhất khi và chỉ khi d ( I ; ( P ) ) = d ( I ; A B ) = IJ
Vậy (P) là mặt phẳng đi qua J và có VTPT IJ →
⇒ ( P ) : x + ( y − 1 ) + ( z − 2 ) = 0 ⇔ − x − y − z + 3 = 0 ⇒ T = − 3
Đáp án B
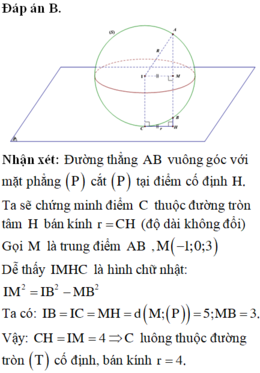
Xét S : x - 1 2 + y - 2 2 + z - 3 2 = 16 có tâm I(1;2;3) bán kính R = 4
Gọi O là hình chiếu của I trên mặt phẳng (P). Ta có S m i n ⇔ d I ; P m a x ⇔ I O m a x
Khi và chỉ khi I O ≡ I H với H là hình chiếu của I trên AB
⇒ I H → là vecto pháp tuyến của mặt phẳng (P) mà I A = I B ⇒ H là trung điểm AB
⇒ H ( 0 ; 1 ; 2 ) ⇒ I H → = ( - 1 ; - 1 ; - 1 ) ⇒ m p P là -x - y - z + 3 = 0.
Đáp án B
Phương pháp:
- Đưa phương trình mặt phẳng (P) về dạng chỉ còn 1 tham số.
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất ó d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Cách giải:
có tâm I(1;2;3) và bán kính R = 5
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Ta có
Ta tìm giá trị lớn nhất của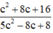
. Gọi m là giá trị của 
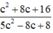với c nào đó.
Ta có:
(*) có nghiệm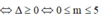
Khi đó