Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(S) có tâm I ( 2;2;2 ), bán kính R = 2 3 . Nhận thấy O và A đều thuộc (S). Tam giác OAB đều, có bán kính đường tròn ngoại tiếp r = O A 3 = 4 2 3
Khoảng cách d ( I; (P) ) = R 2 - r 2 = 2 3
(P) đi qua O có phương trình dạng: ax + by +cz = 0
(P) đi qua A, suy ra b = -a
d ( I; (P) ) = 2 3 ⇔ 2 a + b + c a 2 + b 2 + c 2 = 2 3
⇔ 2 c 2 a 2 + c 2 = 2 3 ⇔ 4 c 2 2 a 2 + c 2 = 4 3 ⇔ 12 c 2 = 8 a 2 + 4 c 2 ⇔ c 2 = a 2 ⇔ c = ± a
Vậy có hai mặt phẳng cần tìm: x - y + z = 0; x - y - z = 0
Đáp án B
Đáp án D
Gọi d = P ∩ Q ,d có VTCP là u → .
Khi đó u → = 1 ; − 1 ; 0 , 2 ; 0 ; 4 = − 4 ; − 4 ; 2 = − 2 2 ; 2 ; − 1 .
Mặt phẳng (R) qua A 1 ; 2 ; 3 , có VTCP là 2 ; 2 ; − 1 và đi qua điểm B ( − 1 2 ; − 1 2 ; 0 ) thuộc giao tuyến, (R) có phương trình là R : x − y + 1 = 0.
Đáp án D
Phương pháp :
Đường thẳng qua A song song với hai mặt phẳng (P); (Q) nhận 
là 1VTCP.
Cách giải : Ta có 
lần lượt là các VTPT của
Ta có :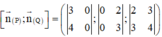
là 1 VTCP của đường thẳng qua A và vuông góc với cả
Vậy phương trình đường thẳng cần tìm là: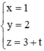 
Với t = -3 ta có đường thẳng đi qua điểm B(1;2;0) => phương trình đường thẳng cần tìm là :
x = 1 y = 2 z = t
