Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Dễ dàng suy ra:
A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , a , b , c > 0
vì d M ; O B C = d M ; O y z = x M = 1 , tương tự ta có được M 1 ; 2 ; 3
M ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 1.2.3 a . b . c 3 ⇔ a b c 6 = V O . A B C ≥ 27
Dấu bằng xảy ra khi:
1 a = 2 b = 3 c = 1 3 ⇒ a = 3 ; b = 6 ; c = 9 ⇒ a + b + c = 18

Đáp án A
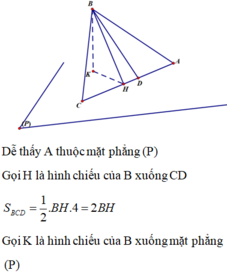
Gọi H là hình chiếu vuông góc của B lên đường thẳng CD, khi đó ta có
![]()
Do đó yêu cầu bài toán trở thành tìm H để khoảng cách BH là lớn nhất hay nhỏ nhất.
Ta thấy BH nhỏ nhất đúng bằng khoảng cách từ B đến mp (P), ta có
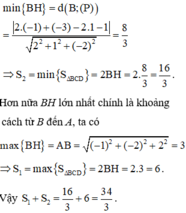

Đáp án là C.
+ Tìm được M m ; m ; n 2 .
+ Ta có:
B M → = 0 ; m ; n 2 ; B D → = − m ; m ; 0 ; B A ' → = − m ; 0 ; n
B M → ; B D → = − m n 2 ; − m n 2 ; m 2 ; B M → ; B D → B A ' → = 3 2 m 2 n
V B M D A ' = 1 6 B M → ; B D → B A ' → = 1 4 m 2 n
mà n = 4 − m ⇒ V B M D A ' = − 1 4 m 3 + m 2 = f m
+ f ' m = − 3 4 m 2 + 2 m = 0 ⇔ m = 0 l o a i m = 8 3 ⇒ f m = 64 27
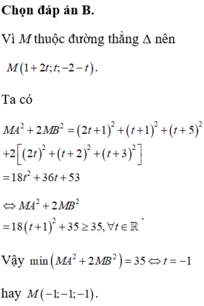
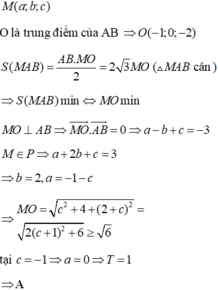


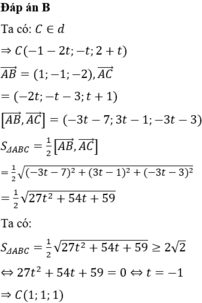
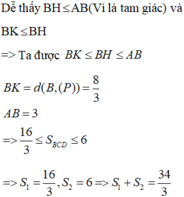

Chọn B.
Đường thẳng AB có phương trình là
Khoảng cách từ O tới đường thẳng AB bằng
Diện tích tam giác OAB đạt giá trị nhỏ nhất bằng 1 khi a = 0