Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(\overrightarrow{MN}=\left(2;2-2\right)=2\left(1;1;-1\right)\)
Phương trình tham số MN: \(\left\{{}\begin{matrix}x=1+t\\y=t\\z=1-t\end{matrix}\right.\)
b. \(\overrightarrow{BC}=\left(2;1;1\right)\Rightarrow d\) nhận (2;1;1) là 1 vtpt
Phương trình d: \(\left\{{}\begin{matrix}x=2t\\y=-1+t\\z=3+t\end{matrix}\right.\)

Đáp án C
Veto chỉ phương ![]()
Đi qua ![]()
Phương trình đường thẳng cần tìm có dạng:
![]()

Đáp án C
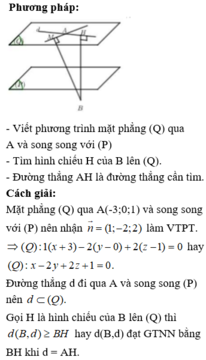
Phương pháp
Gọi H là hình chiếu của B trên mặt phẳng (Q) đi qua A và song song với (P). Khi đó
![]()
![]()
Cách giải
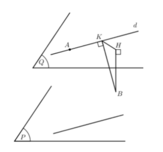
![]()
Gọi (Q) là mặt phẳng đi qua A và song song với (P) ta tìm được phương trình mặt phẳng (Q): (P): x-2y+2z-5=0, khi đó d ∈ (Q)
Gọi H là hình chiếu của B trên (Q) ta có
![]()
![]()
Phương trình đường thẳng d’ đi qua B và vuông góc với (Q) là
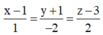
![]()
![]()
![]()
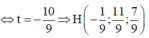
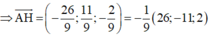
Vậy phương trình đường thẳng d cần tìm là d:
x + 3 26 = y 11 = z - 1 2

Chọn A.
Ta có:
![]()
Vì d song song với BC nên d có vectơ chỉ phương u → 0 ; 1 ; 2
Đường thẳng d qua A(1;4;-1) và có vectơ chỉ phương u → 0 ; 1 ; 2
Vậy phương trình tham số của d là x = 1 y = 4 + t z = - 1 + 2 t

Chọn A.
![]()
Vì d song song với BC nên d có vectơ chỉ phương u → 0 ; 1 ; 2
Đường thẳng d qua A(1;4;-1) và có vectơ chỉ phương u → 0 ; 1 ; 2
Vậy phương trình tham số của d là x = 1 y = 4 + t z = - 1 + 2 t

Chọn D
Đường thẳng d đi qua A nên d (B; d) ≤ BA, do đó khoảng cách từ B đến d lớn nhất khi ![]() , với là vectơ chỉ phương của d.
, với là vectơ chỉ phương của d.

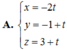


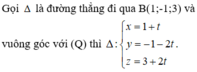
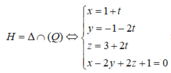
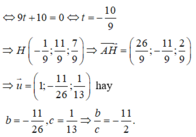
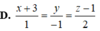

Ta có: \(\overrightarrow{BC}=\left(-1;-6;3\right)\)
Đường thẳng song song với \(BC\) nên nó nhận \(\overrightarrow{BC}\) làm VTCP
\(\Rightarrow\) Phương trình tham số của đường thẳng đi qua \(A\) và song song với \(BC\) là: \(\left\{{}\begin{matrix}x=1-t\\y=-1-6t\\z=3+3t\end{matrix}\right.\quad\left(t\in R\right)\).