Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
Mặt phẳng trung trực của MN và mặt phẳng vuông góc với MN tại trung điểm của MN.
Cách giải: Gọi I là trung điểm của MN ta có: I(2;0;-1)
![]()
=>Mặt phẳng trung trực của MN đi qua và nhận vectơ n → =(1;1;-3) là 1 VTPT, do đó có phương trình :
![]()
![]()

Đáp án B
Ta có M N : x = t y = - 1 - 2 t z = 2 - t .
Gọi H(t;-1-2t;2-t) là hình chiếu vuông góc của K lên MN
Khi đó
H K → = ( t ; - 1 - 2 t ; - t ) . M N → ( - 1 ; 2 ; 1 ) = 0
⇔ t - 2 - 4 t - t = 0 ⇔ t = - 1 3
H K → = ( t ; - 1 - 2 t ; - t ) . M N → ( - 1 ; 2 ; 1 ) = 0
⇒ H - 1 3 ; - 1 3 ; 7 3 . T a c ó d ( K ; ( P ) ) ≤ K H
dấu “=” xảy ra khi KH ⊥ (P)
Khi đó
n → = K H → = - 1 3 ; - 1 3 ; 1 3 = - 1 3 ( 1 ; 1 ; - 1 )

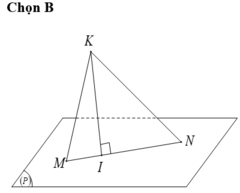
Ta có: ![]() Đường thẳng (d) qua hai điểm M, N có phương trình tham số
Đường thẳng (d) qua hai điểm M, N có phương trình tham số 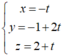
Gọi I là hình chiếu vuông góc của K lên đường thẳng (d) => I (-t; -1 + 2t; 2 + t). Khi đó ta có ![]()
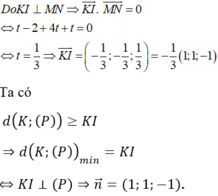

Đáp án B
Mặt phẳng trung trực của MN nhận ![]() làm véc-tơ pháp tuyến và đi qua trung điểm I(2;0;-1) của MN nên nó có phương trình x+y-3z-5=0.
làm véc-tơ pháp tuyến và đi qua trung điểm I(2;0;-1) của MN nên nó có phương trình x+y-3z-5=0.

Đáp án C
Gọi I là trung điểm của BC ⇒ I 5 2 ; - 1 2 ; 1 và E thỏa mãn
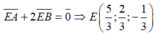
Khi đó
![]()
![]()
Dễ thấy I, E nằm cùng phía với mặt phẳng (Oyz)
Gọi F là điểm đối xứng E qua mp (Oyz) ⇒ F - 5 3 ; 2 3 ; - 1 3
Do đó
![]()
![]()
![]()

Chọn C
Gọi tâm mặt cầu là: I(x;y;0).
I A = I B I A = I C ⇔ ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 1 ) 2 + ( y + 3 ) + 1 2 ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 2 ) 2 + ( y - 2 ) 2 + 3 2 ⇔ ( y - 2 ) 2 + 4 2 = ( y + 3 ) 2 + 1 2 x 2 - 2 x + 1 + 16 = x 2 - 4 x + 4 + 9 ⇔ 10 y = 10 2 x = - 4 ⇔ x = - 2 y = 1 ⇒ i = 2 R = 2 ( - 3 ) 2 + ( - 1 ) 2 + 4 2 = 2 26
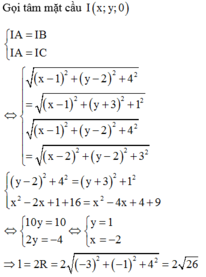

Đáp án C
Lấy đối xứng qua mặt (Oyz) thì x đổi dấu còn y, z giữ nguyên nên N(-3;-1;2).