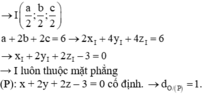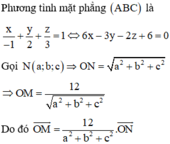
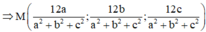

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

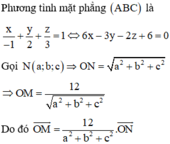
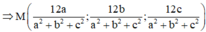


Đáp án A.
1. Tìm tọa độ tâm I ngoại tiếp tứ diện OABC
Gọi M là trung điểm của AB thì M a 2 ; b 2 ; 0 . Đường thẳng d là trục của nên d đi qua M và nhận vecto chỉ phương k → = 0 ; 0 ; 1
Phương trình tham số của đường thẳng d : x = a 2 y = b 2 z = t t ∈ ℝ .
Gọi N là trung điểm của OC thì N 0 ; 0 ; c 2 .
Mặt phẳng (P) là mặt phẳng trung trực của OC nên (P) đi qua M và nhận vecto pháp tuyến là k → = 0 ; 0 ; 1 .
Phương trình tổng quát của mặt phẳng P : z = c 2 .
Khi đó tâm I của mặt cầu ngoại tiếp tứ diện OABC là giao điểm của đường thẳng d và mặt phẳng (P), tức I a 2 ; b 2 ; c 2 .
2. Tìm mặt phẳng (P) là quỹ tích của tâm I và tính d O ; P .
Ta có x I = a 2 ; y I = b 2 ; z I = c 2 ⇒ a = 2 x I b = 2 y I c = 2 z I
Mà a + 2 b + 2 c = 6 nên 2 x I + 2.2 y I + 2.2 z I = 6 ⇔ x I + 2 y I + 2 z I − 3 = 0
Vậy điểm I luôn nằm trên một mp cố định có pt là P : x + 2 y + 2 z − 3 = 0 .
Vậy d O ; P = 0 + 2.0 + 2.0 − 3 1 2 + 2 2 + 2 2 = 1

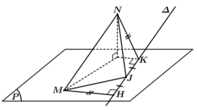
Do đó J thuộc mặt phẳng trung trực của MN là x + y + z - 9 = 0
Lại có ![]()
![]()
Từ đó suy ra J thuộc giao tuyến của hai mặt phẳng có phương trình

Chọn B.

Đáp án A.
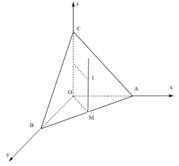
M là trung điểm AB. Qua M kẻ đường thẳng vuông góc với mặt phẳng (OAB) cắt mặt phẳng trung trực của OC tại I. I chính làm tâm đường tròn ngoại tiếp tứ diện OABC