Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
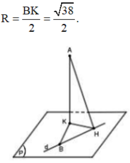
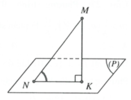
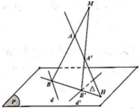
Gọi K là hình chiếu vuông góc của điểm A trên mặt phẳng (P).

Vậy điểm H luôn thuộc đường tròn đường kính BK cố định. Bán kính của đường tròn đó là:

Đáp án B
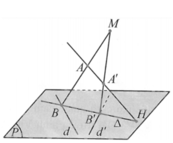
Điểm N ∈ d ⇒ N - 2 + 2 t ; 1 + t ; 1 - t mà A là trung điểm của MN ⇒ M 4 - 2 t ; 5 - t ; 3 + t
Mặt khác M = ∆ ∩ P ⇒ M ∈ P ⇒ 2 4 - 2 t - 5 - t + 3 + t - 10 = 0 ⇔ t = - 2
Khi đó M ( 8 ; 7 ; 1 ) , N ( - 6 ; - 1 ; 3 ) ⇒ M N → = - 14 ; - 8 ; 2 ⇒ M N : x + 6 7 = y + 1 4 = z - 3 - 1 .

Đáp án D
Vì A, B, C lần lượt là hình chiếu vuông góc của M trên trục Ox, Oy, Oz nên: A − 3 ; 0 ; 0 B 0 ; 2 ; 0 C 0 ; 0 ; 4

Em có M’ là hình chiếu song song của M trên (ABC)
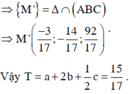







Do đó J thuộc mặt phẳng trung trực của MN là x + y + z - 9 = 0
Lại có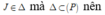
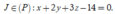
Từ đó suy ra J thuộc giao tuyến của hai mặt phẳng có phương trình
Chọn B.