Trong hình vẽ bên, biết A 1 ^ = 5 7 A 2 ^ , B...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

13 tháng 1 2018

Trong hình vẽ bên, biết A 1 ^ = 5 7 A 2 ^ , B 2 ^ − B 1 ^ = 30 ° và a ⊥ c . Tính C 1 ^ và C 2 ^

#Toán lớp 7

Cao Minh Tâm

13 tháng 1 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

16 tháng 7 2019

Cho hình vẽ bên, biết a // b và B ^ 2 = 45 0 a). Tính số đo A ^ 1 b). So sánh A ^ 3 và B ^ 1 c). Tính A ^ 2 + B 1 ^ ...

Đọc tiếp

#Toán lớp 7

Cao Minh Tâm

16 tháng 7 2019

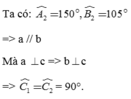
a) Vì B 2 ^ , A 1 ^ là cặp góc trong cùng phía nên ta có:

B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .

b) Ta có B ^ 1 = A ^ 1 = 135 ∘ (hai góc đồng vị)

mà A ^ 3 = A ^ 1 = 135 ∘ (hai góc đối đỉnh)

Vậy B ^ 1 = A ^ 3 = 135 ∘

c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1 (theo câu b)

Do đó A ^ 2 + B ^ 1 = 180 ∘

Đúng(0)

Yukino Ayama

17 tháng 12 2022

Cho hình vẽ bên biết B1=75 độa)chứng minh m//nb)Tính A1 và A2 A B 1 1 1 2 d c ...

Đọc tiếp

#Toán lớp 7

Nguyễn Lê Phước Thịnh

17 tháng 1 2023

a: m vuông góc c

n vuông góc c

=>m//n

b: góc A1=180-75=105 độ

góc A2=180-105=75 độ

Đúng(0)

ĐOÀN THỊ MINH HIỀN

19 tháng 9 2021

bài 1 :tìm x , biết :(x-7)^ x+1(x-7)^x+11=0bài 2 :tìm x , biết :a,|2x-3| > 5 c,|3x-1| ≤ 7 d,|3x-5| + |2x+3| = 7bài 3 :a,tính tổng S = 1 + 5^2 + 5^4 + ....... + 5^200.b,so sánh 2^30 + 3^30 + 4^30 và...

Đọc tiếp

#Toán lớp 7

Pham Trong Bach

15 tháng 6 2017

Cho hình vẽ bên cho biết a // b và A ^ 1 − B ^ 2 = 70 0 . Hãy tính A ^ 3 và B ^ 4

#Toán lớp 7

Cao Minh Tâm

15 tháng 6 2017

+) Vì a // b nên A ^ 1 + B ^ 2 = 180 ∘ (cặp góc trong cùng phía)

Mặt khác A ^ 1 − B ^ 2 = 70 0

⇒ A ^ 1 = 180 ∘ + 70 ∘ : 2 = 125 ∘ và B ^ 2 = 180 ∘ − 125 ∘ = 55 ∘

+) Ta có A ^ 3 = A ^ 1 (hai góc đối đỉnh) mà A ^ 1 = 125 ∘

⇒ A ^ 3 = 125 ∘

Ta có B ^ 2 = B ^ 4 (hai góc đối đỉnh) mà B ^ 2 = 55 ∘

⇒ B ^ 4 = 55 ∘

Đúng(0)

Pham Trong Bach

5 tháng 5 2017

Trong hình vẽ bên, biết A 1 ^ = 5 7 A 2 ^ , B 2 ^ − B 1 ^ = 30° và a ⊥ c. Tính C 1 ^ và C 2 ^

#Toán lớp 7

Cao Minh Tâm

5 tháng 5 2017

Ta có: A 2 ^ = 150 ° , B 2 ^ = 105 ° => a // b

Mà a ⊥ c => bc => C 1 ^ = C 2 ^ = 90°

Đúng(0)

Nga Dayy

1 tháng 12 2021

1. Cho a và b là 2 số tỉ lệ nghịch với 4,5 và b - a = 27. Tính a và b
2. Cho xyz tỉ lệ nghịch với 1/3, 1/2, 1/5 và x + 2y - z = 8. Tìm xyz
3. Tìm a, b, c biết a và b tỉ lệ nghịch với 1/3 và 1/2; a và c tỉ lệ nghịch với 1/5 và 1/7 và a + b + c = 184
giúp mình ạ

#Toán lớp 7

Nguyễn Hoàng Minh

1 tháng 12 2021

\(1,4a=5b\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{b-a}{4-5}=\dfrac{27}{-1}=-27\\ \Leftrightarrow\left\{{}\begin{matrix}a=-135\\b=-108\end{matrix}\right.\\ 2,\dfrac{1}{3}x=\dfrac{1}{2}y=\dfrac{1}{5}z\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x+2y-z}{3+4-5}=\dfrac{8}{2}=4\\ \Leftrightarrow\left\{{}\begin{matrix}x=12\\y=8\\z=20\end{matrix}\right.\\ 3,\dfrac{1}{3}a=\dfrac{1}{2}b;\dfrac{1}{5}a=\dfrac{1}{7}c\\ \Leftrightarrow\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{21}=\dfrac{a+b+c}{15+10+21}=\dfrac{184}{46}=4\\ \Leftrightarrow\left\{{}\begin{matrix}a=60\\b=40\\c=84\end{matrix}\right.\)

Đúng(2)