Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1:
Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)
Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)
\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)
\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)
\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)
Dấu "=" xảy ra khi và chỉ khi:
\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)
\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Cách 2:
Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)
Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:
\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)
Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)
\(\Rightarrow C\left(2;2\right)\)
Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)
Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)
\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD
\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)

Đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=25\) có tâm \(I\left(1;1\right)\) và bán kính \(R=5\)
\(\overrightarrow{IA}=\left(6;8\right)\Rightarrow IA=10=2R\)=> Đường tròn (C) chia đôi IA tại C
Gọi D là trung điểm IC, ta có: \(\frac{ID}{IM}=\frac{1}{2}=\frac{IM}{IA}\)=> \(\Delta\)IDM ~ \(\Delta\)IMA (c.g.c), từ đây MA=2MD
Suy ra \(P=2\left(MD+MB\right)\ge2BD\)(không đổi)
Dấu "=" xảy ra khi M thuộc đoạn BD hay M là giao điểm của đoạn BD với (C)
*) Tìm M:
Ta có: C là trung điểm IA => \(C\left(4;5\right)\), D là trung điểm IC => \(D\left(\frac{5}{2};3\right)\)
\(\overrightarrow{BD}=\left(\frac{5}{2};-5\right)\Rightarrow BD:\hept{\begin{cases}x=\frac{5}{2}t\\y=8-5t\end{cases}}\); vì M thuộc BD nên \(M\left(\frac{5}{2}t;8-5t\right)\)
\(\overrightarrow{IM}=\left(\frac{5}{2}t-1;7-5t\right)\Rightarrow IM^2=\left(\frac{5}{2}t-1\right)^2+\left(7-5t\right)^2=R^2=25\)
\(\Leftrightarrow\orbr{\begin{cases}t=2\\t=\frac{2}{5}\end{cases}}\Rightarrow\orbr{\begin{cases}M\left(5;-2\right)\\M\left(1;6\right)\end{cases}}\)
Nếu \(M\left(5;-2\right)\)thì \(\overrightarrow{MB}=\left(-5;10\right);\overrightarrow{MD}=\left(-\frac{5}{2};5\right)\Rightarrow\overrightarrow{MB}=2\overrightarrow{MD}\)=> M nằm ngoài đoạn BD (L)
Vậy \(M\left(1;6\right)\).

Ta có: A(-1; 2) ∈ (d): 3x + y + 1 = 0.
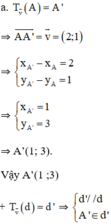
⇒ (d’): 3x + y – 6 = 0.
b. ĐOy (A) = A1 (1 ; 2)
Lấy B(0 ; -1) ∈ d
Ảnh của B qua phép đối xứng trục Oy: ĐOy (B) = B(0; -1) (vì B ∈ Oy).
⇒ d1 = ĐOy (d) chính là đường thẳng A1B.
⇒ d1: 3x – y – 1 = 0.
c. Phép đối xứng tâm O biến A thành A2(1; -2).
d2 là ảnh của d qua phép đối xứng tâm O
⇒ d2 // d và d2 đi qua A2(1 ; -2)
⇒ (d2): 3x + y – 1 = 0.
d. Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.
Q(O;90º) biến N thành N’(-2; 0), biến A thành A’, biến M thành B(0; -1).
Vậy Q(O;90º) biến hình chữ nhật ONAM thành hình chữ nhật ON’A’B. Do đó A’(-2; -1) đi qua A và B, Q(O;90º) biến A thành A’(-2; -1) biến B thành B’(1; 0)
Vậy Q(O;90º) biến d thành d’ qua hai điểm A’, B’
Do đó phương trình d’ là :
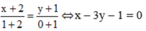

Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
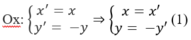
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9

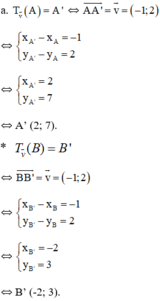
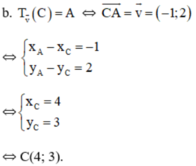
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
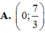
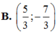
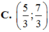
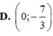
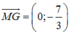
Gọi `M(x;3/2x+5/2)`
Ta có:`|\vec{MA}-2\vec{MB}|`
`=|(4-x;7-3/2x-5/2)-2(2-x;1-3/2x-5/2)|`
`=|(x;3/2x+17/2)|`
`=\sqrt{x^2+(3/2x+17/2)^2}`
`=\sqrt{x^2+9/4x^2+51/2x+289/4}`
`=\sqrt{13/4x^2+51/2x+289/4}`
`=\sqrt{(\sqrt{13}/2 x+[51\sqrt{13}]/26)^2+289/13} >= [17\sqrt{13}]/13`
Dấu "`=`" xảy ra `<=>\sqrt{13}/2x+[51\sqrt{13}]/26=0<=>x=-51/13`
`=>M(-51/13;-44/13)`