Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)
Áp dụng định lý Pitago:
\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)
\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)
Mặt khác do G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)

Đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=25\) có tâm \(I\left(1;1\right)\) và bán kính \(R=5\)
\(\overrightarrow{IA}=\left(6;8\right)\Rightarrow IA=10=2R\)=> Đường tròn (C) chia đôi IA tại C
Gọi D là trung điểm IC, ta có: \(\frac{ID}{IM}=\frac{1}{2}=\frac{IM}{IA}\)=> \(\Delta\)IDM ~ \(\Delta\)IMA (c.g.c), từ đây MA=2MD
Suy ra \(P=2\left(MD+MB\right)\ge2BD\)(không đổi)
Dấu "=" xảy ra khi M thuộc đoạn BD hay M là giao điểm của đoạn BD với (C)
*) Tìm M:
Ta có: C là trung điểm IA => \(C\left(4;5\right)\), D là trung điểm IC => \(D\left(\frac{5}{2};3\right)\)
\(\overrightarrow{BD}=\left(\frac{5}{2};-5\right)\Rightarrow BD:\hept{\begin{cases}x=\frac{5}{2}t\\y=8-5t\end{cases}}\); vì M thuộc BD nên \(M\left(\frac{5}{2}t;8-5t\right)\)
\(\overrightarrow{IM}=\left(\frac{5}{2}t-1;7-5t\right)\Rightarrow IM^2=\left(\frac{5}{2}t-1\right)^2+\left(7-5t\right)^2=R^2=25\)
\(\Leftrightarrow\orbr{\begin{cases}t=2\\t=\frac{2}{5}\end{cases}}\Rightarrow\orbr{\begin{cases}M\left(5;-2\right)\\M\left(1;6\right)\end{cases}}\)
Nếu \(M\left(5;-2\right)\)thì \(\overrightarrow{MB}=\left(-5;10\right);\overrightarrow{MD}=\left(-\frac{5}{2};5\right)\Rightarrow\overrightarrow{MB}=2\overrightarrow{MD}\)=> M nằm ngoài đoạn BD (L)
Vậy \(M\left(1;6\right)\).

a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .
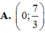
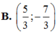
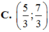
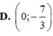
ĐÁP ÁN: D