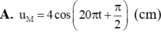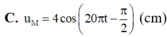Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

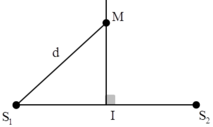
Giả sử S1S2 = 2d, điểm M cách trung điểm I một đoạn x có biên độ 1cm.
Bước sóng: \(\lambda=\frac{v}{f}=\frac{40}{20}=2cm\)
Giả sử sóng do S1 đến M lệch pha hơn sóng do S2 đến M là \(\varphi\), ta có: \(\varphi=\frac{4\pi x}{\lambda}\)
Biên độ của M là tổng hợp 2 dao động do S1 và S2 đến, ta có: \(6^2+8^2+2.6.8.\cos\varphi=1\Rightarrow\cos\varphi=\frac{-99}{96}
Bạn làm sai rồi nhé, kia là mm và cm, đề này chuẩn
Đáp án 0,25 nhé baby ![]()

\(\lambda=\frac{v}{f}=\frac{30}{15}=2cm\)
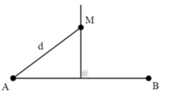
Vì 2 nguồn cùng pha nên số điểm dao động với biên độ cực đại trên đoạn AB thỏa mãn:
\(-AB< k\lambda< AB\)
\(\Leftrightarrow\) -8,2 < 2k < 8,2
\(\Leftrightarrow\)\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;^+_-4\)
Vậy có 9 điểm dao động với biên độ cực đại trên đoạn AB.
Số điểm dao động với biên độ cực tiểu trên đoạn AB thỏa mãn:
\(-AB< \left(k+0,5\right)\lambda< AB\)
\(\Leftrightarrow\) -8,2 < (k+0,5).2 < 8,2
\(\Leftrightarrow\) -4,6 < k < 3,6
\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;-4\)
Vậy có 8 điểm có biên độ dao động cực tiểu trên đoạn AB.

Đáp án A
Ta có ω = 20π → f = 10Hz → λ = v/f = 3 cm.
→ AB = 40 cm = 13λ + λ/3.
Những điểm dao động với biên độ 3 2 cm cách nút những khoảng λ/4.
→ Trên AB có số điểm dao động với biên độ 3 2 cm là: 13.4 + 2 = 54 điểm.

Đáp án C
+ Bước sóng của sóng λ = v f = 30 15 = 2Hz
→ Số điểm cực đại trên S1S2 là - S 1 S 2 λ ≤ k ≤ S 1 S 2 λ ⇔ - 11 2 ≤ k ≤ 11 2 ⇔ - 5 , 5 ≤ k ≤ 5 , 5 → có 11 điểm.