Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha

+ ΔABD = ΔCBD (g.c.g) vì:
∠ABD = ∠CBD (gt)
BD chung
∠ADB = ∠BDC (= 90o)
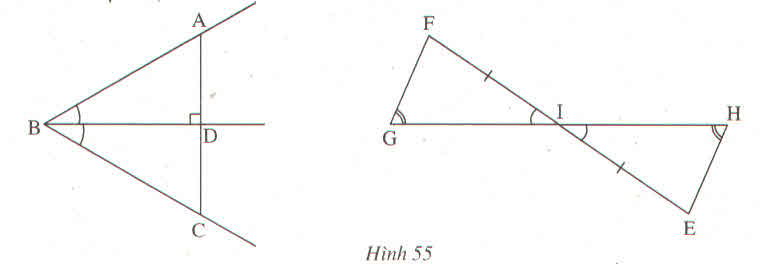
+ Ta có: ∠FGI = ∠IHE ( giả thiết). Mà hai góc này ở vị trí so le trong nên: FG // HE
⇒ ∠GFI = ∠IEH ( hai góc so le trong).
*) Khi đó: ΔGIF = ΔHIE (g.c.g) vì:
∠GFI = ∠IEH ( chứng minh trên)
FI = IE ( giả thiết)
∠GIF = ∠EIH (hai góc đối đỉnh)

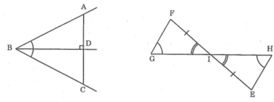
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH

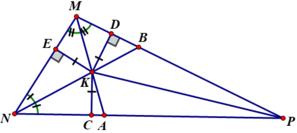
Điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau Theo định lí ⇒ K là giao điểm của các đường phân giác trong tam giác MNP.
Vì vậy ta chỉ cần vẽ phân giác của hai trong ba góc của ∆MNP.
Cách vẽ :
- Vẽ ΔMNP
- Vẽ đường phân giác của hai góc M và N : MA là phân giác góc M ; NB là phân giác góc B
Chúng cắt nhau tại K
- K là điểm cần vẽ
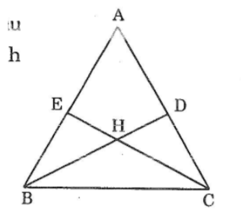


Có ba cặp tam giác bằng nhau:
ΔABD=ΔACE
ΔBEC=ΔCDB
ΔBEH=ΔCDH