

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi x, y là hai số cần tìm.
Vì tổng của hai số bằng 59 nên ta có phương trình: x + y = 59
Vì hai lần của số này bé hơn ba lần của số kia là 7 nên ta có phương trình: 3y – 2x = 7.
Ta có hệ phương trình: 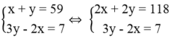
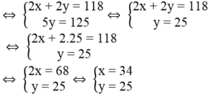
Vậy hai số cần tìm là 34 và 25

Gọi 2 số cần tìm là x; y.
Tổng của 2 số là 59 nên ta có: x + y = 54
Ba lần số này hơn số kia là 2 nên: 3x – y =2
Ta có hệ phương trình:
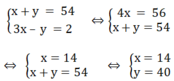
Vậy hai số cần tìm là 14 và 40.

Gọi x, y là 2 số đó.
Tổng của hai số bằng 23, ta có:
x + y = 23 (1)
2 lần số này lớn hơn số kia 1 đơn vị, ta có:
2x - y = 1 (2)
Từ (1), (2) có hệ phương trình: \(\left\{{}\begin{matrix}x+y=23\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=46\\2x-y=1\end{matrix}\right.\\ \Leftrightarrow3y=45\\ \Rightarrow y=15\Rightarrow x=\dfrac{1+15}{2}=8\)
Vậy 2 số đó là 15 và 8

Tổng hai số = 59
=> x + y = 59 (1)
2 lần số này bé hơn 3 lần số kia là 57
=> -2x + 3y = 57 (2)
Từ (1) và (2) ta được hệ phương trình:
{x + y = 59
{-2x + 3y = 57
<=> {x = 24
{y = 35

Gọi số thứ nhất là : x
số thứ 2 là : y
\(\Rightarrow x+y=150\)
\(\frac{x}{9}+\frac{y}{3}=42\)
Sr bấm nhầm
Gọi số thứ nhất là x ; số thứ 2 là y
\(\Rightarrow\hept{\begin{cases}x+y=150\\\frac{x}{9}+\frac{y}{3}=42\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y=150\\\frac{9x}{9}+\frac{9y}{3}=378\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y=150\\x+3y=378\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2y=228\\x+y=150\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}y=114\\x=36\end{cases}}\)
Vậy số thứ nhất là 36
số thứ 2 là 114

Gọi số thứ nhất là x
Số thứ hai là 27-x
Theo đề, ta có: 3x-2(27-x)=21
=>3x-54+2x=21
=>5x=75
hay x=15
Vậy: Hai số cần tìm là 15 và 12