Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y là 2 số đó.
Tổng của hai số bằng 23, ta có:
x + y = 23 (1)
2 lần số này lớn hơn số kia 1 đơn vị, ta có:
2x - y = 1 (2)
Từ (1), (2) có hệ phương trình: \(\left\{{}\begin{matrix}x+y=23\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=46\\2x-y=1\end{matrix}\right.\\ \Leftrightarrow3y=45\\ \Rightarrow y=15\Rightarrow x=\dfrac{1+15}{2}=8\)
Vậy 2 số đó là 15 và 8

Gọi x, y là hai số cần tìm.
Vì tổng của hai số bằng 59 nên ta có phương trình: x + y = 59
Vì hai lần của số này bé hơn ba lần của số kia là 7 nên ta có phương trình: 3y – 2x = 7.
Ta có hệ phương trình: 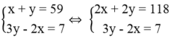
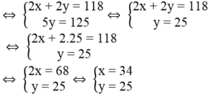
Vậy hai số cần tìm là 34 và 25

Gọi chữ số hàng chục là x (x là các số tự nhiên từ 1 tới 9)
Gọi chữ số hàng đơn vị là y (y là các số tự nhiên từ 0 tới 9)
\(\Rightarrow\) Giá trị của số đó là: \(10x+y\)
Do số đó bằng tổng các chữ số cộng với 9 nên:
\(10x+y=x+y+9\Rightarrow9x=9\Rightarrow x=1\)
Số đó bằng 2 lần hiệu 2 chữ số của nó và cộng thêm 20:
Trường hợp 1: \(10x+y=2\left(x-y\right)+20\)
\(\Rightarrow10.1+y=2-2y+20\)
\(\Rightarrow3y=12\Rightarrow y=4\)
Trường hợp 2: \(10x+y=2\left(y-x\right)+20\)
\(\Rightarrow10.1+y=2y-2+20\)
\(\Rightarrow y=-8< 0\) (loại)
Vậy số đó là 14

Gọi số có 2 chữ số cần tìm có dạng là ab(Điều kiện: \(a,b\in N\); 0<a<10; \(1\le b< 10\))
Vì tổng các chữ số bằng 9 nên ta có phương trình: a+b=9(1)
Vì 8 lần chữ số này bằng chữ số kia nên ta có phương trình: 8a=b(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=9\\8a=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+8a=9\\b=9-a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9a=9\\b=9-a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=8\end{matrix}\right.\)(thỏa ĐK)
Vậy: Số cần tìm là 18


Gọi số thứ nhất là : x
số thứ 2 là : y
\(\Rightarrow x+y=150\)
\(\frac{x}{9}+\frac{y}{3}=42\)
Sr bấm nhầm
Gọi số thứ nhất là x ; số thứ 2 là y
\(\Rightarrow\hept{\begin{cases}x+y=150\\\frac{x}{9}+\frac{y}{3}=42\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y=150\\\frac{9x}{9}+\frac{9y}{3}=378\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y=150\\x+3y=378\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2y=228\\x+y=150\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}y=114\\x=36\end{cases}}\)
Vậy số thứ nhất là 36
số thứ 2 là 114