K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 9 2021
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}\cdot\dfrac{2ax-2a^2-4ax}{x\left(x-a\right)}\)
\(=\dfrac{a\left(x-a\right)}{x+a}\cdot\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{a}{x+a}\cdot\dfrac{-2a\left(a+x\right)}{x}\)
\(=\dfrac{-2a^2}{x}\)
HP
7 tháng 9 2021
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}.\dfrac{2a\left(x-a\right)-4ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{-2a\left(a+x\right)}{x\left(x-a\right)}\)
\(=2a\)
13 tháng 9 2020
Dung à mày (:
Ta có \(\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a}{x+1}+\frac{b}{\left(x+1\right)^2}+\frac{c}{x+2}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x+1\right)\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{b\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x+1\right)^2}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x^2+3x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{bx+2b}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x^2+2x+1\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{ax^2+3ax+2a+bx+2b+cx^2+2cx+c}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Rightarrow1=x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)\)
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}a+c=0\\3a+b+2c=0\\2a+2b+c=1\end{cases}}\)=> Chịu :)) Khó quá không làm được ... Hoặc do đề sai ;-;
13 tháng 9 2020
Không sai == Trong sách Nâng cao và phát triển toán 8 tập 1 trang 33 bài 123 ý c
T cũng chịu '-'
HP
1
25 tháng 10 2021
a) Xét tứ giác AEBC có:
M là trung điểm AB(gt)
M là trung điểm EC(E đối xứng C qua M)
=> AEBC là hình bình hành
b) Xét tứ giác AFCB có:
N là trung điểm AC(gt)
N là trung điểm BF(B đối xứng F qua N)
=> AFCB là hình bình hành
=> AF//BC
Mà AE//BC(AEBC là hình bình hành)
=> E,A,F thẳng hàng(tiên đề Ơ-Clit)
c) Ta có: AE=BC(AEBC là hình bình hành)
AF=BC(AFCB là hình bình hành)
=> EF=AE+AF=2BC\(\Rightarrow BC=\dfrac{1}{2}EF\)
Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm AC(gt)
=> MN là đường trung bình
\(\Rightarrow MN=\dfrac{1}{2}BC\Rightarrow MN=\dfrac{1}{2}.\dfrac{1}{2}EF=\dfrac{1}{4}EF\Rightarrow\dfrac{MN}{EF}=\dfrac{1}{4}\)
d) Để BCFE là hthang cân thì:
\(\widehat{BEA}=\widehat{AFC}\Rightarrow\widehat{ABC}=\widehat{ACB}\)
=> Tam giác ABC cân tại A
9 tháng 5 2017
Dễ hiểu mà bạn mấy cái dạng này mk gặp nhiều lần rồi
Ta có:\(\left(2x+1\right)\left(x-1\right)-2x^2+mx+m-2=0\)
Nhân ra thôi mà bạn:\(2x^2-2x+x-1-2x^2+mx+m-2=0\)
\(\Rightarrow-x-3+mx+m=0\)(Sao ko giống cái ở trên vậy hay là bạn giải sai kiểm tra lại đi rồi hãy nói)
9 tháng 5 2017
bạn có cần phải kiêu căng vậy không? là sách giải bạn nhé :)))
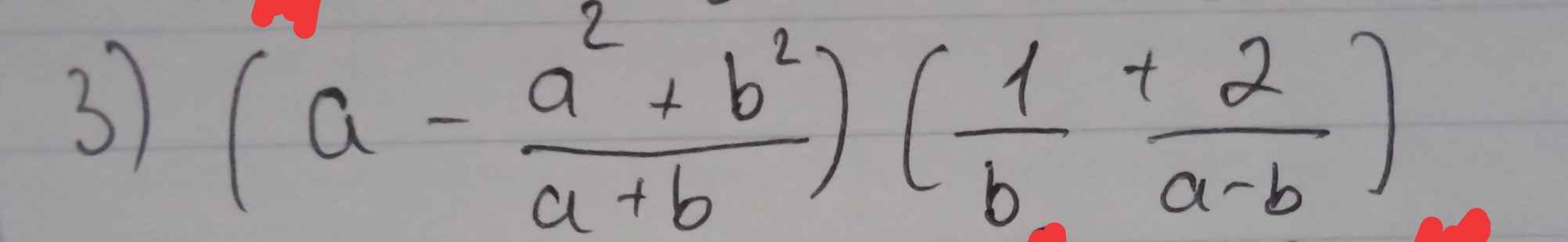
\(\left(a-\dfrac{a^2+b^2}{a+b}\right)\left(\dfrac{1}{b}+\dfrac{2}{a-b}\right)\)
\(=\dfrac{a^2+ab-a^2-b^2}{a+b}\cdot\dfrac{a-b+2b}{b\left(a-b\right)}\)
\(=\dfrac{b\left(a-b\right)}{a+b}\cdot\dfrac{a+b}{b\left(a-b\right)}\)
=1