Question

[Hồng Phúc Nguyễn]

Mọi người giúp mình với không làm tắt không chép mạng

Answer 1

[Lấp La Lấp Lánh]

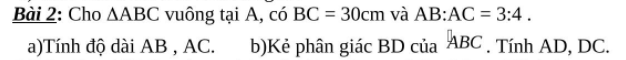
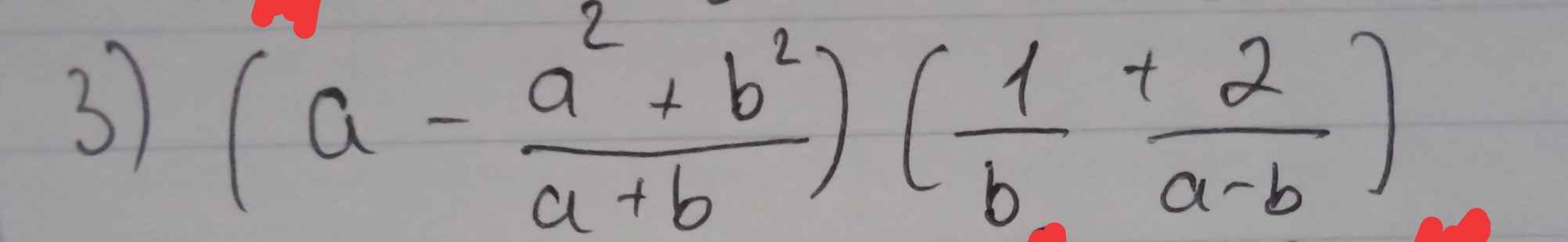
a) Xét tứ giác AEBC có:

M là trung điểm AB(gt)

M là trung điểm EC(E đối xứng C qua M)

=> AEBC là hình bình hành

b) Xét tứ giác AFCB có:

N là trung điểm AC(gt)

N là trung điểm BF(B đối xứng F qua N)

=> AFCB là hình bình hành

=> AF//BC

Mà AE//BC(AEBC là hình bình hành)

=> E,A,F thẳng hàng(tiên đề Ơ-Clit)

c) Ta có: AE=BC(AEBC là hình bình hành)

               AF=BC(AFCB là hình bình hành)

=> EF=AE+AF=2BC\(\Rightarrow BC=\dfrac{1}{2}EF\)

Xét tam giác ABC có:

M là trung điểm AB(gt)

N là trung điểm AC(gt)

=> MN là đường trung bình

\(\Rightarrow MN=\dfrac{1}{2}BC\Rightarrow MN=\dfrac{1}{2}.\dfrac{1}{2}EF=\dfrac{1}{4}EF\Rightarrow\dfrac{MN}{EF}=\dfrac{1}{4}\)

d) Để BCFE là hthang cân thì:

\(\widehat{BEA}=\widehat{AFC}\Rightarrow\widehat{ABC}=\widehat{ACB}\)

=> Tam giác ABC cân tại A