GA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
2
22 tháng 9 2021
Bài 5:
a) \(A=x^2-4x+9=\left(x^2-4x+4\right)+5=\left(x-2\right)^2+5\ge5\)
\(minA=5\Leftrightarrow x=2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=2x^2-6x=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
\(minC=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\)
Bài 4:
a) \(M=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxM=7\Leftrightarrow x=2\)
b) \(N=x-x^2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(maxN=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(P=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxP=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)
KN
1 tháng 4 2018
D = \(-\dfrac{5}{x^2-4x+7}\)
Vì: x2 - 4x + 7
= x2 - 4x + 4 + 3
= (x - 2)2 + 3 \(\ge\) 3 \(\forall\)x
\(\Rightarrow\) \(\dfrac{5}{\left(x-2\right)^2+3}\) \(\le\) \(\dfrac{5}{3}\) \(\forall\)x
\(\Rightarrow\) \(-\dfrac{5}{\left(x-2\right)^2+3}\)\(\ge\)-\(\dfrac{5}{3}\) \(\forall\)x
Dấu"=" xảy ra khi:
x - 2 = 0
\(\Rightarrow\) x = 2
Vậy.............
E = \(\dfrac{2x^2+4x+4}{x^2+2x+4}\)
Ta có:
\(\dfrac{2x^2+4x+4}{x^2+2x+4}\)
= \(\dfrac{2\left(x^2+2x+4\right)-4}{x^2+2x+4}\)
= 2 - \(\dfrac{4}{x^2+2x+4}\)
Vì:
x2 + 2x + 4
= x2 + 2x + 1 + 3
= (x + 1)2 + 3 \(\ge\) 3 \(\forall\)x
\(\Rightarrow\) \(\dfrac{4}{\left(x+1\right)^2+3}\) \(\le\) \(\dfrac{4}{3}\) \(\forall\)x
\(\Rightarrow\) 2 - \(\dfrac{4}{\left(x+1\right)^2+3}\) \(\le\) \(\dfrac{2}{3}\) \(\forall\)x
Dấu "=" xảy ra khi:
x + 1 = 0
\(\Rightarrow\) x = -1
Vậy...............
F = \(\dfrac{6x+8}{x^2+1}\)
= \(\dfrac{x^2+6x+9-x^2-1}{x^2+1}\)
= \(\dfrac{\left(x+3\right)^2-\left(x^2+1\right)}{x^2+1}\)
= \(\dfrac{\left(x+3\right)^2}{x^2+1}-1\) \(\ge\) -1 \(\forall\)x
Dấu "=" xảy ra khi:
(x + 3)2 = 0
\(\Rightarrow\) x + 3 = 0
\(\Rightarrow\) x = -3
Vậy.....................
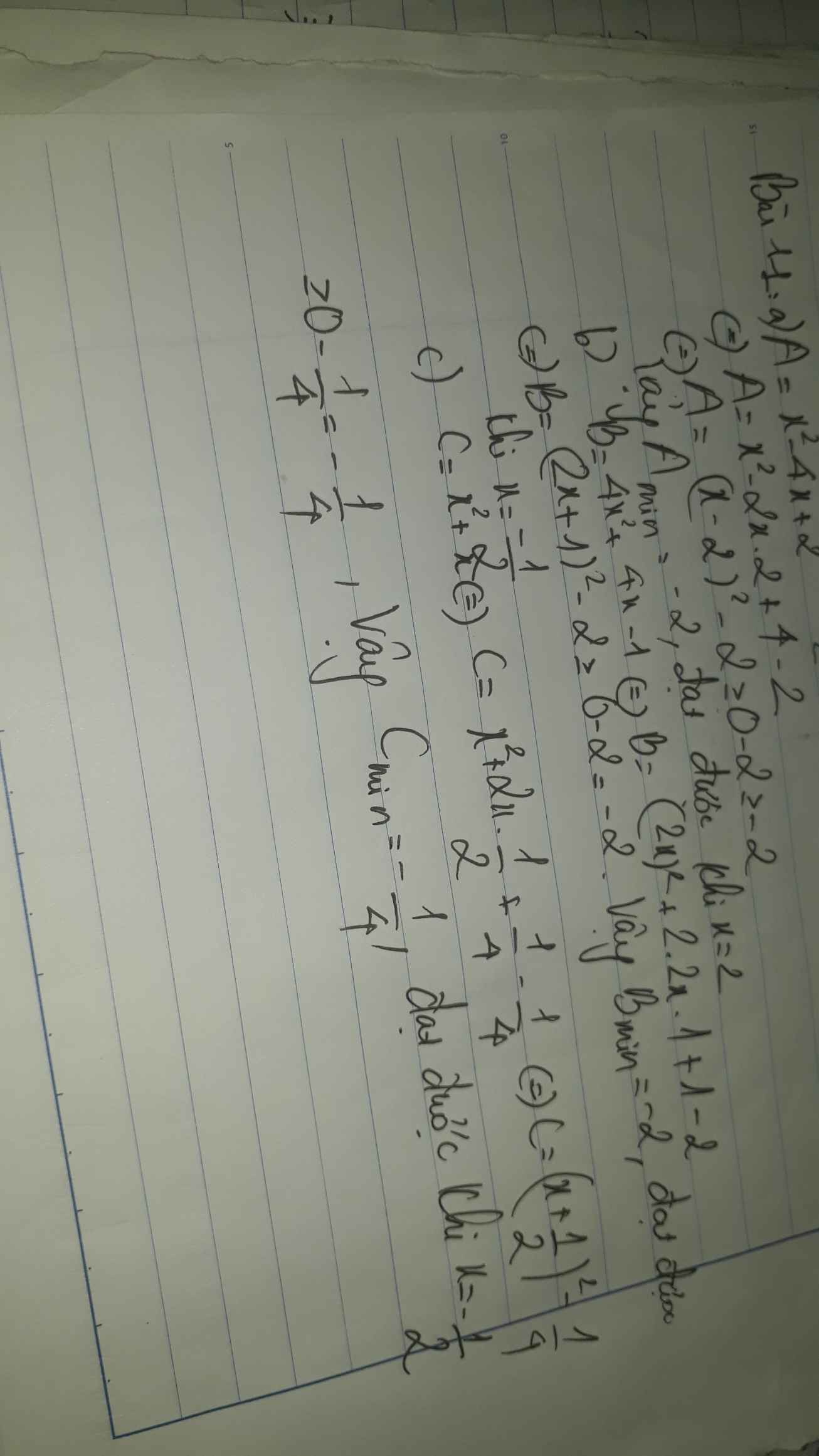
a A=4x-x^2+3
=(x-2)^2-1
MIN A= -1 khi (x-2)^2=0
x-2=0
x=2
B=x-x^2
B=-x^2+x
-B=x^2-x
-B=(x-1/2)^2-1/4
B=-(x-1/2)^2+1/4
MAX B=1/4 khi -(x-1/2)^2=0
x-1/2=0
x=1/2
N=2x-2x^2-5
-N=2x^2-2x+5
-N=2(x^2-x+2)+1
-N=2{(x-1/2)^2+7/4}+1
-N=2(x-1/2)^2+7/2+1
-N=2(x-1/2)^2+9/2
N=-2(x-1/2)^2-9/2
MAX N=-9/2 khi -2(x-1/2)^2=0
x-1/2=0
x=1/2