ND
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 10 2021
\(a,A=\left(x^2-x\right)\left(x^2-x-12\right)\\ A=\left(x^2-x\right)^2-12\left(x^2-x\right)\\ A=\left(x^2-x\right)^2-12\left(x^2-x\right)+36-36\\ A=\left(x^2-x+6\right)^2-36\ge-36\\ A_{min}=-36\Leftrightarrow x^2-x+6=0\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\\ b,B=4x^4+4x^3+5x^2+4x+3\\ B=\left(4x^4+4x^3+x^2\right)+\left(x^2+4x+4\right)-1\\ B=x^2\left(2x+1\right)^2+\left(x+2\right)^2-1\ge-1\\ B_{min}=-1\Leftrightarrow\left\{{}\begin{matrix}x\left(2x+1\right)=0\\x+2=0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
Vậy dấu \("="\) không xảy ra
12 tháng 10 2018
Thực hiện phép chia ta được thương là: \(2x^2+2x+1\)
Đặt \(A=2x^2+2x+1=2\left(x^2+x+\frac{1}{4}\right)+\frac{1}{2}=2\left(x+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\forall x\)
Dấu "=" xảy ra khi: \(x+\frac{1}{2}=0\Rightarrow x=-\frac{1}{2}\)
Chúc bạn học tốt.
DH
2
7 tháng 7 2021
a,\(A=\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=\left(x^2+6x+5\right)\left(x^2+6x+8\right)\)
đặt \(x^2+6x+5=t=>t\left(t+3\right)=t^2+3t=t^2+2.\dfrac{3}{2}t+\dfrac{9}{4}-\dfrac{9}{4}\)
\(=\left(t+\dfrac{3}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}< =>t=\dfrac{-3}{2}\)
\(=>A\)\(=-\dfrac{3}{2}\left(-\dfrac{3}{2}+3\right)=-2,25\)
Vậy Min A\(=-2,25\)
b,\(B=-x^2-4x-9y^2-6y-6\)
\(=-\left(x^2+4x+4\right)-\left(3y\right)^2-2.3y-1-1\)
\(=-\left(x+2\right)^2-\left(3y+1\right)^2-1\le-1\)
dấu"=' xảy ra\(< =>x=-2,y=-\dfrac{1}{3}\)
AH
Akai Haruma
Giáo viên
7 tháng 7 2021
a.
$(x+1)(x+2)(x+4)(x+5)=(x+1)(x+5)(x+2)(x+4)=(x^2+6x+5)(x^2+6x+8)$
$=a(a+3)$ với $a=x^2+6x+5$
$=a^2+3a=(a^2+3a+\frac{9}{4})-\frac{9}{4}$
$=(a+\frac{3}{2})^2-\frac{9}{4}$
$=(x^2+6x+\frac{13}{2})^2-\frac{9}{4}\geq \frac{-9}{4}$
Vậy gtnn của biểu thức là $\frac{-9}{4}$. Giá trị này đạt tại $x^2+6x+\frac{13}{2}=0$
$\Leftrightarrow x=\frac{-6\pm \sqrt{10}}{2}$
16 tháng 8 2021
a: Ta có: \(A=\left(2x+3\right)\left(4x^2-6x+9\right)-2\left(4x^3-1\right)\)
\(=8x^3+27-8x^3+2\)
=29
b: Ta có: \(B=\left(64x^3-1\right)-\left(4x-3\right)\left(16x^2+3\right)\)
\(=64x^3-1-64x^3-12x-48x^2+9\)
\(=-12x+8\)
c: Ta có: \(2\left(x^3+y^3\right)-3\left(x^2+y^2\right)\)
\(=2\left(x^2+xy+y^2\right)-3\left(-2xy\right)\)
\(=2x^2+2xy+2y^2+6xy\)
\(=2x^2+8xy+2y^2\)
30 tháng 8 2021
1) \(A=36x^2+12x+1=\left(6x+1\right)^2\ge0\)
\(minA=0\Leftrightarrow x=-\dfrac{1}{6}\)
2) \(B=9x^2+6x+1=\left(3x+1\right)^2\ge0\)
\(minB=0\Leftrightarrow x=-\dfrac{1}{3}\)
4) \(D=x^2-4x+y^2-8y+6=\left(x-2\right)^2+\left(y-4\right)^2-14\ge-14\)
\(minD=-14\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\)
30 tháng 8 2021
3) \(C=\left(x+1\right)\left(x-2\right)\left(x-3\right)\left(x-6\right)=\left(x^2-5x-6\right)\left(x^2-5x+6\right)=\left(x^2-5x\right)^2-36\ge-36\)
\(minC\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
5) \(E=\left(x-8\right)^2+\left(x+7\right)^2=2x^2-2x+113=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{225}{2}\ge\dfrac{225}{2}\)
\(minE=\dfrac{225}{2}\Leftrightarrow x=\dfrac{1}{2}\)
GA
1
27 tháng 8 2016
a A=4x-x^2+3
=(x-2)^2-1
MIN A= -1 khi (x-2)^2=0
x-2=0
x=2
B=x-x^2
B=-x^2+x
-B=x^2-x
-B=(x-1/2)^2-1/4
B=-(x-1/2)^2+1/4
MAX B=1/4 khi -(x-1/2)^2=0
x-1/2=0
x=1/2
N=2x-2x^2-5
-N=2x^2-2x+5
-N=2(x^2-x+2)+1
-N=2{(x-1/2)^2+7/4}+1
-N=2(x-1/2)^2+7/2+1
-N=2(x-1/2)^2+9/2
N=-2(x-1/2)^2-9/2
MAX N=-9/2 khi -2(x-1/2)^2=0
x-1/2=0
x=1/2
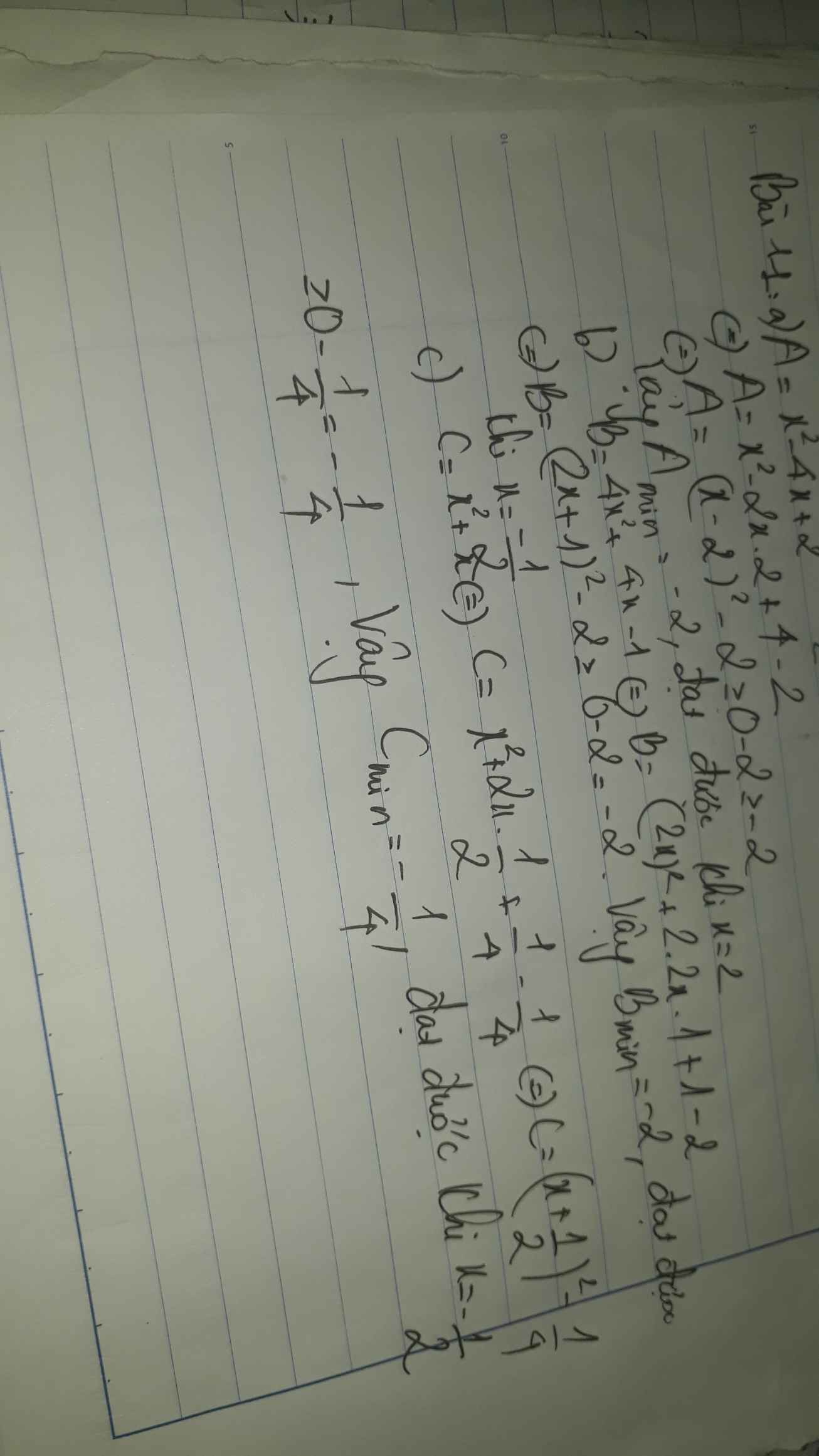
tu lam
bạn chia ra thui có kq mmk làm cho