
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


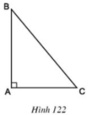
Đo hai cạnh góc vuông, ta được AB = 30mm, AC = 25mm.
Áp dụng công thức tính diện tích tam giác vuông, ta được:
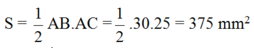
Vậy S = 375 mm2

a: Sxq=(6+8)*2*5=10*14=140cm2
Stp=140+2*6*8=236cm2
V=6*8*5=240cm3
b: Xét ΔMNH vuông tại H và ΔPMQ vuông tại Q có
góc NMH=góc MPQ
=>ΔMHN đồng dạng với ΔPMQ
c: NH=6*8/10=4,8cm

Gọi ba cạnh của tam giác đo lần lượt là \(a;b;c\) và 3 đường cao tương ứng là \(ha;hb;hc\)
Ta có:
\(Sabc=\frac{1}{2}a.ha=\frac{1}{2}b.hb=\frac{1}{2}c.hc\)
\(\Leftrightarrow\) \(a.ha=b.hb=c.hc\)
\(\Leftrightarrow\) \(\frac{a}{\frac{1}{ha}}=\frac{b}{\frac{1}{hb}}=\frac{c}{\frac{1}{hc}}\)
\(\Leftrightarrow\) \(a:b:c=\frac{1}{ha}:\frac{1}{hb}:\frac{1}{hc}\) hay \(a:b:c=\frac{1}{9,6}:\frac{1}{12}:\frac{1}{16}\)
\(\Leftrightarrow\) \(a:b:c=5:4:3\)
Vì 3 cạch của tam giác tỉ lệ với 5;4;3 nên tam giác sẽ đồng dạng với tam giác có ba cạch \(a'=5;b'=4;c'=3\)
Áp dụng công thức Hê-rong ta có:
\(Sa'b'c'=\sqrt{\frac{5+4+3}{2}\left(\frac{5+3+4}{2}-5\right)\left(\frac{5+4+3}{2}-4\right)\left(\frac{5+4+3}{2}-3\right)}\)
\(\Leftrightarrow\) \(Sa'b'c'=\sqrt{36}=6\)
\(\Leftrightarrow\) \(ha'=\frac{6.2}{5}=2,4\)
Lại có:
\(\frac{Sabc}{Sa'b'c'}=\left(\frac{9,6}{2.4}\right)^2=4^2=16\)
\(\Leftrightarrow\) \(Sabc=16.6=96\left(cm^2\right)\)
Vậy...............


a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
bn ơi câu a bn giải thích ra luôn giùm mik ik
câu b,c nx

tự vẽ hình
ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)
Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)
=> <HBA=<HAC
Xét tam giác BAH và ACH
<BHA=<AHC\(\left(90^0\right)\)
<ABH=<HAC
=> Tam giác BAH đồng dạng với tam giác ACH
=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm
b, ta có BC=BH+CH=4+9=13 cm
S(ABC) = AH*BC=36*13=468 cm\(^2\)
Gọi a là cạnh đối diện góc A, tương tự đối với b và c. Gọi chiều cao tương ứng với cạnh a là ha, tương tự đối với hb và hc. Ta có ha.a=hb.b=hc.c=2S, từ ha.a=hb.b => a/b=hb/ha=65/60=13/12 => đặt a=13k (k khác 0), b=12k (k khác 0). Từ hb.b=hc.c => b/c=hc/hb=156/65=12/5 => đặt c=5k (k khác 0), nhận thấy a;b và c thỏa mãn Pytago => theo định lý Pytago đảo thì tam giác ABC vuông tại A. Giả sử AH,BK,CL là đường cao từ các đỉnh. Theo hệ thức lượng trong tam giác vuông ta có AC^2=CH.BC CH=(AC^2)/BC = 144k/13. Xét tam giác ACH có góc H=90 độ, nên áp dụng định lý Pytago ta có AH^2 + CH^2 = AC^2 => AC^2 - CH^2 = AH^2 (12k)^2 - (144k/13)^2 = 60^2, sau đó ta tính được k=13 => AB=65mm; AC=156mm => diện tích ABC = (65 x 156 )/ 2 = 5070 mm^2
à há bài hay đấy