Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
a: Ta có: \(\left|x+\dfrac{19}{5}\right|+\left|y+\dfrac{1890}{1975}\right|+\left|z-2004\right|=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{19}{5}=0\\y+\dfrac{1890}{1975}=0\\z-2004=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{19}{5}\\y=-\dfrac{378}{395}\\z=2004\end{matrix}\right.\)
b: \(\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{3}{2}\right|+\left|x-y-z-\dfrac{1}{2}\right|=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y+\dfrac{3}{2}=0\\x-y-z-\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{3}{2}\\z=\dfrac{3}{2}\end{matrix}\right.\)

b) Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{-6}=\frac{2x-3y+z}{2.2-3.5+\left(-6\right)}=\frac{34}{-17}=-\frac{34}{17}=-2\)
\(\frac{x}{2}=-2\Rightarrow x=\left(-2\right).2=-4\)
\(\frac{y}{5}=-2\Rightarrow y=\left(-2\right).5=-10\)
\(\frac{z}{-6}=-2\Rightarrow z=\left(-2\right).\left(-6\right)=12\)
Vậy x=-4 ; y=-10 và z=12
a) \(\frac{x}{-4}=\frac{y}{6}=\frac{z}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{-4}=\frac{z}{7}=\frac{y}{6}\Rightarrow\frac{z-x}{7-\left(-4\right)}=\frac{12}{11}\)
\(\frac{x}{-4}=\frac{12}{11}\Rightarrow x=-\frac{48}{11}\)
\(\frac{z}{7}=\frac{12}{11}\Rightarrow z=\frac{84}{11}\)
\(\frac{y}{6}=\frac{12}{11}\Rightarrow y=\frac{72}{11}\)
b) \(\frac{x}{2}=\frac{y}{5}=\frac{z}{-6}\Rightarrow\frac{2x}{4}=\frac{3y}{15}=\frac{z}{-6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{4}=\frac{3y}{15}=\frac{z}{-6}=\frac{2x-3y+z}{4-15-6}=\frac{34}{-17}=-2\)
\(\frac{2x}{4}=-2\Rightarrow2x=-8\Rightarrow x=-4\)
\(\frac{3y}{15}=-2\Rightarrow3y=-30\Rightarrow y=-10\)
\(\frac{z}{-6}=-2\Rightarrow z=12\)

a) \(\left|1-x\right|+\left|y-\frac{2}{3}\right|+\left|x+z\right|=0\)
\(\Leftrightarrow\hept{\begin{cases}1-x=0\\y-\frac{2}{3}=0\\x+z=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=1-0=1\\y=0+\frac{2}{3}=\frac{2}{3}\\z=0-1=-1\end{cases}}}\)
Vậy \(x=1,y=\frac{2}{3},z=-1\)
b) \(\left|\frac{1}{4}-x\right|+\left|x+y+z\right|+\left|\frac{2}{3}+y\right|=0\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{4}-x=0\\x+y+z=0\\\frac{2}{3}+y=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{4}-0=\frac{1}{4}\\x+y+z=0\\y=0+\frac{2}{3}=\frac{2}{3}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{1}{4}\\z=0-\frac{1}{4}-\frac{2}{3}=\frac{-11}{12}\\y=\frac{2}{3}\end{cases}}}\)
Vậy \(x=\frac{1}{4},y=\frac{-11}{12},z=\frac{2}{3}\)

x(x+y+z) + y(x+y+z) + z(x+y+z) = 2 + 25 - 2 = 25
=> ( x+ y+ z )(x+y+z) = 25
=> x + y+ z = 5 hoặc x + y +z = -5
(+) x + y +z = 5 => x.5 = 2 => x = 2/5
=> y.5=5 => y = 1
=> z.5 = -2 => z = -2/5
(+) x+ y+ z = -5 => -5x = 2 => x= -2/5 (loại x > 0)
Vậy x = 2/5 ; y = 1 ; z = -2/5
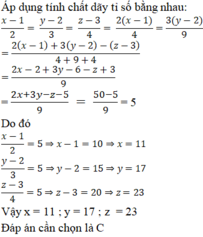
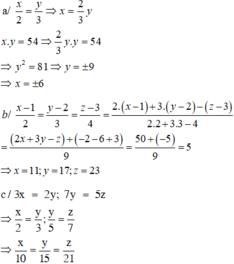
a) Vì : \(\left|x+\frac{19}{5}\right|\ge0\forall x\in R\)
\(\left|y+\frac{1890}{1975}\right|\ge0\forall y\in R\)
\(\left|z-2004\right|\ge0\forall z\in R\)
\(\Rightarrow\left|x+\frac{19}{5}\right|+\left|y+\frac{1890}{1975}\right|+\left|z-2004\right|\ge0\forall x,y,z\in R\)
Dấu''='' xảy ra khi và chỉ khi \(\hept{\begin{cases}x=\frac{-19}{5}\\y=\frac{-1890}{1975}\\z=2004\end{cases}}\)
b,\(\left|x+\frac{9}{2}\right|+\left|y+\frac{4}{3}\right|+\left|z+\frac{7}{2}\right|\le0\)
Ta có:\(\left|x+\frac{9}{2}\right|\ge0\forall x\)
\( \left|y+\frac{4}{3}\right|\ge0\forall y\)
\(\left|z+\frac{7}{2}\right|\ge0\forall z\)
\(\Rightarrow\left|x+\frac{9}{2}\right|+\left|y+\frac{4}{3}\right|+\left|z+\frac{7}{2}\right|\ge0\forall x,y,z\)
Mà \(\left|x+\frac{9}{2}\right|+\left|y+\frac{4}{3}\right|+\left|z+\frac{7}{2}\right|\le0\)
\(\Rightarrow\left|x+\frac{9}{2}\right|+\left|y+\frac{4}{3}\right|+\left|z+\frac{7}{2}\right|=0\)
\(\Rightarrow\hept{\begin{cases}\left|x+\frac{9}{2}\right|=0\\\left|y+\frac{4}{3}\right|=0\\\left|z+\frac{7}{2}\right|=0\end{cases}\Rightarrow\hept{\begin{cases}x+\frac{9}{2}=0\\y+\frac{4}{3}=0\\z+\frac{7}{2}=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-\frac{9}{2}\\y=-\frac{4}{3}\\z=-\frac{7}{2}\end{cases}}}\)