Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x2 - 4y2 tại x = 102 , y = \(\dfrac{1}{2}\)
= x2 - (2y)2
= (x - 2y)(x + 2y)
Thay x = 102 , y = \(\dfrac{1}{2}\) vào , ta có :
(x - 2y)(x + 2y)
= (102 - 2.\(\dfrac{1}{2}\))(102 + 2 . \(\dfrac{1}{2}\))
= 101 . 103
= 10403
b)Bạn xem lại đề b),c) có bị thiếu không, nên mình bổ sung thêm nhé :
8x3 + 12x2 + 6x + 1 tại x = \(\dfrac{29}{2}\)
= (2x)3 + 3.(2x2).1 + 3.2x.1 + 1
= (2x + 1)3
Thay x = \(\dfrac{29}{2}\) vào , ta có :
(2x + 1)3
= (2.\(\dfrac{29}{2}\) + 1)3
= (29 + 1)3
= 27000
c) x3 - 6x + 12x - 1 tại x = 102
= x3 - 3.x2.2 + 3.x.22 - 23
= (x - 2)3
Thay x = 102 vào , ta có :
(x - 2)3
= (102 - 2)3
= 1000000
Chúc bạn học tôt

\(a,PT\Leftrightarrow x^3-6x^2+12x-8-x^3+x+6x^2-18x-10=0\)
\(\Leftrightarrow-5x-18=0\)
\(\Leftrightarrow x=-\dfrac{18}{5}\)
Vậy ...
\(b,PT\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+10=0\)
\(\Leftrightarrow12x+6=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy ...
\(c,PT\Leftrightarrow\left(x+1\right)^3+3^3=0\)
\(\Leftrightarrow\left(x+1+3\right)\left(x^2+2x+1-3x-3+9\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x^2-x+7\right)=0\)
Thấy : \(x^2-\dfrac{2.x.1}{2}+\dfrac{1}{4}+\dfrac{27}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}>0\)
\(\Rightarrow x+4=0\)
\(\Leftrightarrow x=-4\)
Vậy ...
\(d,PT\Leftrightarrow\left(x-2\right)^3+1^3=0\)
\(\Leftrightarrow\left(x-2+1\right)\left(x^2-4x+4-x+2+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+7\right)=0\)
Thấy : \(x^2-5x+7=x^2-\dfrac{5.x.2}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)
\(\Rightarrow x-1=0\)
\(\Leftrightarrow x=1\)
Vậy ...

Bài 2:
a: \(A=\left[a+\left(b-c\right)\right]^2+\left[a-\left(b-c\right)\right]^2\)
\(=a^2+2a\left(b-c\right)+\left(b-c\right)^2+a^2-2a\left(b-c\right)+\left(b-c\right)^2\)
\(=2a^2+2\left(b-c\right)^2\)
\(=2\cdot1^2+2\left(3+1\right)^2=2+32=34\)
b: \(B=a^2+2ab+b^2-a^2+2ab-b^2=4ab=4\cdot2\cdot5=40\)

\(a,\Leftrightarrow\left(x+3\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-12x+36\right)=0\\ \Leftrightarrow x\left(x-6\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
a, (x+3)2 - ( 2x + 1 ).( x+3)=0 b, x3-12x2+36x =0
=> (x+3).(x+3-2x-1) => x(x2-12x+36) = 0
=>(x+3).(-x+2) => x(x-6)2 = 0
=> x+3=0 <=> x=-3 => x=0 <=> x=0
-x+2=0 <=> x=-2 x-6= 0 <=> x=6

\(\Leftrightarrow\left(x-2\right)^3=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)

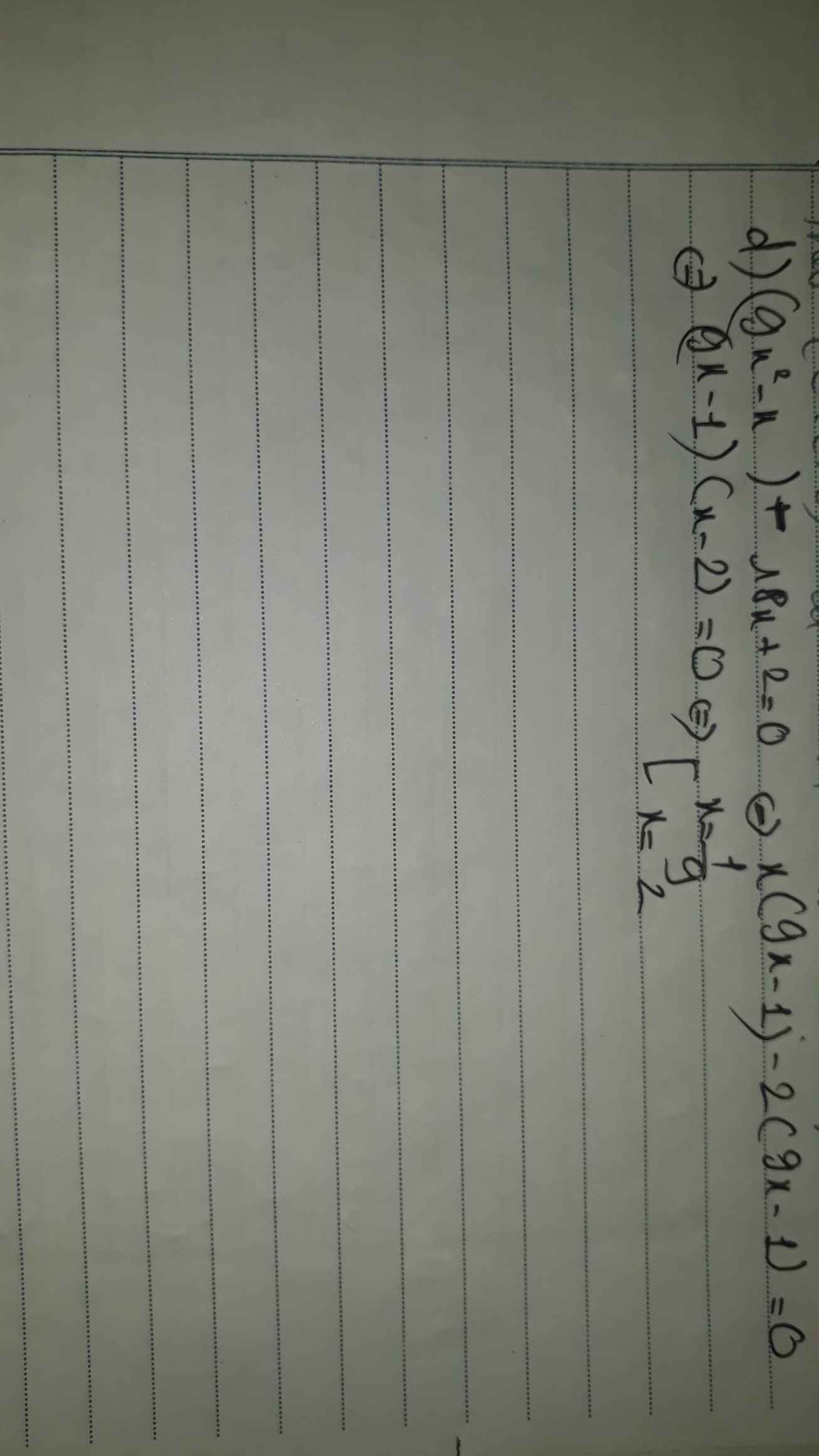
a) (x-2)3 - 6(x+1)2 - x3 + 12 = 0
<=> x3-6x2+12x-8-6(x2+2x+1)-x3+12=0
<=> x3-6x2+12x-8-6x2-12x-6-x3+12=0
<=> -12x2+4=0
<=> \(x=\frac{1}{\sqrt{3}},x=-\frac{1}{\sqrt{3}}\)
vậy pt có 2 nghiệm....
b) x3 - 6x2 + 12x - 8 = 0
<=> (x3-2x2)-(4x2-8x)+(4x+8)=0
<=> (x-2)(x2-4x+4)=(x-2)3=0
=> x=2 là nghiệm
c) 8x3 - 12x2 + 6x - 1 = 0
<=> (2x-1)3=0
<=> x=1/2
a) \(\left(x-2\right)^3-6\left(x+1\right)^2-x^3+12=0\)
\(\Leftrightarrow x^3-6x^2+12x-8-6\left(x^2+2x+1\right)-x^3+12=0\)
\(\Leftrightarrow x^3-6x^2+12x-8-6x^2-12x-6-x^3+12=0\)
\(\Leftrightarrow-12x^2-2=0\)
\(\Leftrightarrow-2\left(6x^2+1\right)=0\)
\(\Leftrightarrow6x^2+1=0\) (vô nghiệm)
Vậy không có giá trị nào của x thỏa mãn pt
b) \(x^3-6x^2+12x-8=0\)
\(\Leftrightarrow\left(x-2\right)^3=0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy x=2
c) \(8x^3-12x^2+6x-1=0\)
\(\Leftrightarrow\left(2x-1\right)^3=0\)
\(\Leftrightarrow2x-1=0\Leftrightarrow x=\frac{1}{2}\)
Vậy \(=\frac{1}{2}\)