Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét điểm \(M\left(m;0\right)\in Ox\).
Đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=k\left(x-m\right)\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}-x^3+3x+2=k\left(x-m\right)\\-3x^2+3=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(3\left(x^2-1\right)\left(x-m\right)-\left(x^3-3x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2-3\left(1+m\right)x+3m\right)-\left(x+1\right)\left(x^2-x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[2x^2-\left(3m+2\right)x+3m+2\right]=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\2x^2-\left(3x+2\right)x+3m+2=0\left(a\right)\end{array}\right.\)
Để từ M kẻ được 3 tiếp tuyến thì (a) phải có 2 nghiệm phân biệt khác -1
\(\begin{cases}\Delta=\left(3m+2\right)\left(3m-6\right)>0\\3m+3\ne0\end{cases}\)\(\Leftrightarrow\begin{cases}m< -\frac{2}{3}Vm>2\\m\ne-1\end{cases}\) (*)
Gọi \(x_1;x_2\) là 2 nghiệm của (a), khi đó hệ số góc của 3 tiếp tuyến là :
\(k_1=-3x_1^2+3;k_2=-3x_2^2+3;k_3=0\)
Để 2 trong 3 tiếp tuyến này vuông góc với nhau \(\Leftrightarrow k_1.k_2=-1\)
\(\Leftrightarrow9\left(x^2_1-1\right)\left(x^2_2-1\right)=1\Leftrightarrow9x^2_1x^2_2-9\left(x_1+x_2\right)^2+18x_1x_2+8=0\left(i\right)\)
Mặt khác, theo định lý Viet, \(x_1+x_2=\frac{3m+2}{2};x_1x_2=\frac{3m+2}{2};\)
Từ đó (i) \(\Leftrightarrow9\left(3m+2\right)+8=0\Leftrightarrow m=-\frac{26}{27}\) thỏa mãn điều kiện (*)
Vậy \(M\left(-\frac{26}{27};0\right)\) là điểm cần tìm

Xét \(M\left(0;m\right)\in Oy\), đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=kx+m\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=kx+m\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2x}{\left(x-1\right)^2}+m\Leftrightarrow\left(m-1\right)x^2-2\left(m+1\right)x+m+1=0\) (*)
Để từ M chỉ kẻ được đúng một tiếp tuyến đến đồ thị hàm số đã cho \(\Leftrightarrow\) (*) có đúng 1 nghiệm.
Do (*) không có nghiêm x = 1 nên (*) có đúng 1 nghiệm
\(\Leftrightarrow\left[\begin{array}{nghiempt}m=1\\\Delta'=2m+2=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}m=1\\m=-1\end{array}\right.\)
Vậy có 2 điểm \(M_1\left(0;1\right);M_2\left(0;-1\right)\) thỏa mãn bài toán

Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)

Xét : \(M\left(x_0;x_0+1+\frac{1}{x_0+1}\right)\)
Tiếp tuyến tại M có phương trình \(y=\left(1-m^2\right)x+m^2+2m+1\) (với \(m=\frac{1}{x_0-1}\))
tiếp tuyến cắt tiệm cận đứng tại \(A\left(1;2m+2\right)\); cắt tiệm cận tại \(B\left(1+\frac{2}{m};2+\frac{2}{m}\right)\) và hai tiệm cận cắt nhau tại I(1;2)
Chu vi tam giác ABI : \(P=AB+BI+IA=\sqrt{4m^2+\frac{8}{m^2}+8}+\frac{2\sqrt{2}}{\left|m\right|}+2\left|m\right|\)
Áp dụng Bất đẳng thức Côsi, ta có :
\(4m^2+\frac{8}{m^2}\ge8\sqrt{2};\frac{2\sqrt{2}}{\left|m\right|}+2\left|m\right|\ge4\sqrt[4]{2}\Rightarrow P\ge\sqrt{8\sqrt{2}+8}+4\sqrt[4]{2}\)
Đẳng thức xảy ra \(\Leftrightarrow m=\pm\sqrt[4]{2}\)
Vậy \(M\left(1\pm\frac{1}{\sqrt[4]{2}};2\pm\frac{1}{\sqrt[4]{2}}\pm\sqrt[4]{2}\right)\)

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.

+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 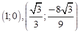 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
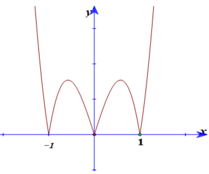
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
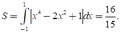
Chọn D.

Tập xác định : \(D=R\backslash\left\{1\right\}\)
\(M\in Ox\Rightarrow M\left(x_0;0\right)\) đường thẳng qua M với hệ số góc k có phương trình \(y=k\left(x-x_0\right)\) \(\left(\Delta\right)\)
\(\left(\Delta\right)\) là tiếp tuyến của đồ thì khi hệ \(\begin{cases}\frac{x^2}{x-1}=k\left(x-x_0\right)\\\frac{x^2-2x}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
\(\Rightarrow\frac{x^2}{x-1}=\frac{x^2-2x}{\left(x-1\right)^2}\left(x-x_0\right)\Leftrightarrow x\left[\left(x_0+1\right)x-2x_0\right]=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=0\\x=\frac{2x_0}{x_0+1}\end{array}\right.\) với \(x_0\ne-1\)
* Với \(x_0=0\Rightarrow k=0\)
* Với \(x_0=\frac{2x_0}{x_0+1}\Rightarrow k=\frac{-4x_0}{\left(x_0+1\right)^2}\)* Để thỏa mãn yêu cầu bài toán thì :\(\tan45^0=\left|\frac{k_1-k_2}{1+k_1k_2}\right|\Rightarrow\frac{4x_0}{\left(x_0+1\right)^2}=\pm1\)\(\Rightarrow x_0=3\pm2\sqrt{2}\)\(\Rightarrow M_1\left(3+2\sqrt{2};0\right);M_2\left(3-2\sqrt{2};0\right)\)