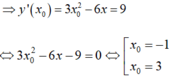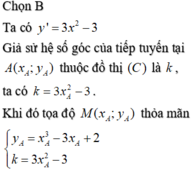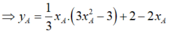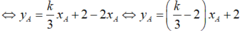Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Kí hiệu d là tiếp tuyến của đồ thị hàm số và (x0;y0) là tọa độ của tiếp điểm.
Ta có: d vuông góc với đường thẳng y =
-
1
45
x
+
2018
nên 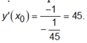
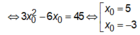
Với ![]() => phương trình tiếp tuyến của đồ thị là: y = 45(x-5) + 52 = 45x - 173
=> phương trình tiếp tuyến của đồ thị là: y = 45(x-5) + 52 = 45x - 173
Với ![]() => phương trình tiếp tuyến của đồ thị là: y = 45(x+3) - 52 = 45x + 83
=> phương trình tiếp tuyến của đồ thị là: y = 45(x+3) - 52 = 45x + 83

Phương trình hoành độ giao điểm của hai đồ thị:
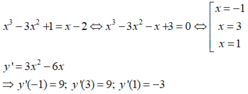
Ba tiếp tuyến tại giao điểm của đồ thị hàm số với đường thẳng y = x - 2 có tổng các hệ số góc là: 9 + 9 + (-3) = 15.
Chọn A.

Tiếp tuyến của đồ thị hàm số có hệ số góc là
k = y ' = 3 x 2 - 6 x = ( 3 x 2 - 6 x + 3 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀x ∈ R
Trong các tiếp tuyến tại các điểm trên đồ thị hàm số, tiếp tuyến có hệ số góc nhỏ nhất bằng -3.
Chọn A

+ Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x= 2 có dạng:
∆: y= k( x-2) hay y= kx-2k
+ ∆ là tiếp tuyến của (C)
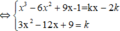
có nghiệm

+ Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k . Vậy có một tiếp tuyến.
+ Dễ thấy kẻ từ một điểm bất kì trên đường thẳng x=2có dạng y= a song song với trục Ox cũng chỉ kẻ được một tiếp tuyến.
Chọn B.