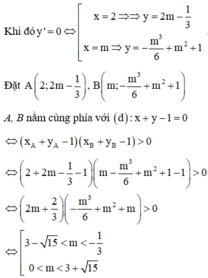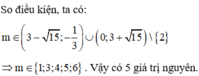Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
TXĐ: D = ℝ .
Ta có y ' = x 2 − 2 m − 1 x + m − 1 .
Để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung thì
m − 1 2 − m − 1 > 0 m − 1 > 0 2 m − 1 > 0 ⇔ m > 2.
Vậy m>2 thỏa mãn điều kiện đề bài.

Đáp án A
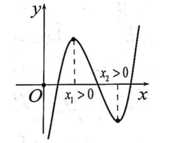
Ta có y ' = x 2 − 2 x + m − 1
Đồ thị hàm số có 2 điểm cực trị đều nằm bên trái trục tung khi y ' = 0 có 2 nghiệm phân biệt đều dương
⇔ Δ ' = 1 − m + 1 > 0 S = 2 > 0 P = m − 1 > 0 ⇔ 2 > m > 1

Đáp án C
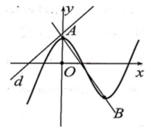
Ta có y ' = 3 m − 3 x 2 + 4 m 2 − m − 1 x + m + 4.
Đồ thị hàm số có 2 điểm cực trị nằm về hai phía trục O y ⇔ y ' = 0 có hai nghiệm trái dấu.
Suy ra x 1 x 2 < 0 ⇔ m + 4 3 m − 3 < 0 ⇔ − 4 < m < 3. m ∈ ℤ ⇒ m ∈ − 3 ; − 2 ; − 1 ; 0 ; 1 ; 2 .