Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp: Tìm điều kiện để phương trình hoành độ giao điểm có ba nghiệm phân biệt thỏa mãn x A = 2 , hoặc x B < - 1 < x C < 1 hoặc - 1 < x B < 1 < x C
Cách giải:
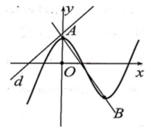
Đồ thị hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 luôn đi qua điểm A(2;0)
Xét phương trình hoành độ giao điểm
x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 = 0
![]()
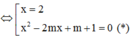
Để phương trình có 3 nghiệm phân biệt ó pt (*) có 2 nghiệm phân biệt khác 2
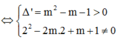
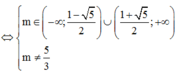
Giả sử x B ; x C ( x B < x C ) là 2 nghiệm phân biệt của phương trình (*).
Để hai điểm B, C một điểm nằm trong một điểm nằm ngoài đường tròn x2 + y2 = 1
TH1: ![]()
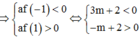
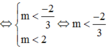
TH2: ![]()
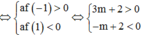
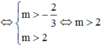
Kết hợp điều kiện ta có: 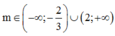
Lại có m ∈ [–10;100]
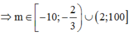
=> Có 108 giá trị m nguyên thỏa mãn yêu cầu bái toán

Đáp án C
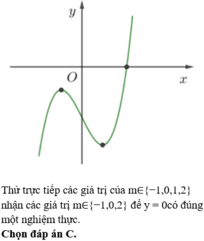
TXĐ: D = ℝ .
Ta có y ' = x 2 − 2 m − 1 x + m − 1 .
Để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung thì
m − 1 2 − m − 1 > 0 m − 1 > 0 2 m − 1 > 0 ⇔ m > 2.
Vậy m>2 thỏa mãn điều kiện đề bài.
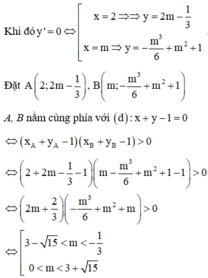
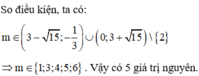







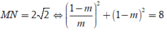
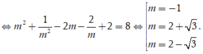
Đáp án B