NH
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
3
VH
25 tháng 12 2020
Ta có: n+3 chia hết cho n-1
mà: n-1 chia hết cho n-1
suy ra:[(n+3)-(n-1)]chia hết cho n-1
(n+3-n+1)chia hết cho n-1
4 chia hết cho n-1
suy ra n-1 thuộc Ư(4)
Ư(4)={1;2;4}
suy ra n-1 thuộc {1;2;4}
Ta có bảng sau:
n-1 1 2 4
n 2 3 5
Vậy n=2 hoặc n=3 hoặc n=5
26 tháng 12 2021
a,
Ta có: 4n-5 chia hết cho 2n-1
=>4n-2-3 chia hết cho 2n-1
=>2.(2n-1)-3 chia hết cho 2n-1
=>3 chia hết cho 2n-1
=>2n-1=Ư(3)=(-1,-3,1,3)
=>2n=(0,-2,2,4)
=>n=(0,-1,1,2)
Vậy n=0,-1,1,2
28 tháng 10 2021
a) \(\left(n+6\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+5⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;4\right\}\)
b) \(\left(4n+9\right)⋮\left(2n+1\right)\Rightarrow2\left(2n+1\right)+7⋮\left(2n+1\right)\)
\(\Rightarrow\left(2n+1\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;3\right\}\)
22 tháng 11 2020
a, \(2n+7⋮n+1\)
\(2\left(n+1\right)+5⋮n+1\)
\(5⋮n+1\)hay \(n+1\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
| n + 1 | 1 | -1 | 5 | -5 |
| n | 0 | -2 | 4 | -6 |
b, \(4n+9⋮2n+3\)
\(2\left(2n+3\right)+3⋮2n+3\)
\(3⋮2n+3\)hay \(2n+3\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| 2n + 3 | 1 | -1 | 3 | -3 |
| 2n | -2 | -4 | 0 | -6 |
| n | -1 | -2 | 0 | -3 |
VB
1
TT
20 tháng 12 2020
a/
\(n+3⋮n-1\)
\(\Leftrightarrow4⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(4\right)=\left\{1;-1;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;2;-3;5\right\}\)
Mà n là stn
\(\Leftrightarrow n\in\left\{0;2;5\right\}\)
b/ \(4n+3⋮2n+1\)
\(\Leftrightarrow2\left(2n+1\right)+1⋮2n+1\)
\(\Leftrightarrow1⋮2n+1\)
\(\Leftrightarrow2n+1\inƯ\left(1\right)=\left\{1;-1\right\}\)
Mà n là số tự nhiên
=> 2n + 1 là số tự nhiên
=> 2n + 1 = 1
=> 2n = 0
=> n = 0
Q
7
S
16 tháng 6 2019
\(a,n+3⋮n-1\)
\(\Rightarrow n-1+4⋮n-1\)
Mà \(n-1⋮n-1\)
\(\Rightarrow n-1\inƯ\left(4\right)\)
\(\Rightarrow n-1\in\left\{\pm1;\pm2;\pm4\right\}\)
\(\Rightarrow n\in\left\{2;0;3;-1;5;-3\right\}\)
~Study well~
#SJ
16 tháng 6 2019
a) \(n+3⋮n-1\)
\(\Rightarrow n-1+4⋮n-1\)
Mà \(n-1⋮n-1\)
\(\Rightarrow4⋮n-1\)
\(\Rightarrow n-1\inƯ\left(4\right)=\left\{\pm1;\pm2\right\}\)
Tìm nốt n
TM
6
PL
5 tháng 9 2021
a) \(n+3⋮n-1\)
\(n-1+4⋮n-1\)
\(\Rightarrow4⋮n-1\)
\(\Rightarrow n-1\inƯ\left(4\right)=\left\{1;2;4;-1;-2;-4\right\}\)
\(\Rightarrow n\in\left\{2;3;5;0;-1;-3\right\}\)
mà \(n\in N\Rightarrow n\in\left\{2;3;5;0\right\}\)
TM
2
L
31 tháng 8 2021
a/
n+3⋮n−1n+3⋮n−1
⇔4⋮n−1⇔4⋮n−1
⇔n−1∈Ư(4)={1;−1;4;−4}
⇔n∈{0;2;−3;5}
Mà n là stn
⇔n∈{0;2;5}
b/ 4n+3⋮2n+1
⇔2(2n+1)+1⋮2n+1
⇔1⋮2n+1
⇔2n+1∈Ư(1)={1;−1}
Mà n là số tự nhiên
=> 2n + 1 là số tự nhiên
=> 2n + 1 = 1
=> 2n = 0
=> n = 0
k cho mik nha
31 tháng 8 2021
a) \(\Rightarrow\)n + 3 \(⋮\)n + 1
n + 1 \(⋮\)n + 1
\(\Rightarrow\)\(=\frac{n+1+2}{n+1}\)
\(\Rightarrow\)\(=\frac{n+1}{n+1}+\frac{2}{n+1}\)
\(\Rightarrow\)\(2⋮n+1\)
\(\Rightarrow\)\(n+1\notin\)Ư(2)
Ta có bảng sau :
| n+1 | -1 | 1 | -2 | 2 |
| n | -2 | 0 | -3 | 1 |
NG
1
LN
28 tháng 6 2018
a) n+3 chia hết cho n-1
=>n-1+4 chia hết cho n-1
=> 4 chia hết cho n-1
Ta có bảng sau:
| n-1 | 1 | 2 | 4 | -1 | -2 | -4 |
| n | 2 | 3 | 5 | 0 | -1 | -1 |
vì n là số tự nhiên nên n thuộc tập hợp {2, 3, 5, 0}
b) 4n+3 chia hết cho 2n+1
=> 4n+2+1 chia hết cho 2n+1
=>1 chia hết cho 2n+1
Ta có bảng sau:
| 2n+1 | 1 | -1 |
| n | 0 | -1 |
vì n là số tự nhiên nên n=0
chúc bạn học tốt nha
ủng hộ mk với nha
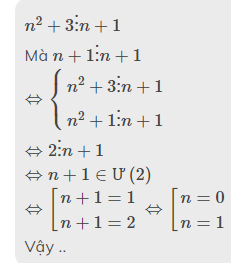
a / n + 3 = (n - 1 )+ 4 vì ( n - 1 ) chia hết ( n - 1 ) => 4 phải chia hết ( n - 1 )
ƯỚC của 4 là : 4 ; 2 ; 1 hay ( 5 - 1 ) ; ( 3 - 1 ) ; ( 2 - 1 )
nên n nhận các giá trị : 5 ; 3 và 2
b/ 4n + 3 = (4n - 2) + 5 = 2 ( 2n - 1 ) + 5
cũng như phần trên có 2 ( 2n - 1 ) chia hết ( 2n - 1) => 5 phải chia hết cho 2n + 1
các Ưcủa 5 là : 5 và 1 vậy nếu 2n - 1 = 5 => n = (5 + 1) : 2 = 3
2n - 1 = 1 => n = ( 1 + 1 ) : 2 = 1
nên n nhận các giá trị là : 3 và 1
a/ Nếu n + 3 chia hết cho n - 1 thì n - 1 + 4 chia hết cho n - 1
Vì n - 1 + 4 chia hết cho n - 1
n - 1 chia hết cho n - 1
=> 4 chia hết cho n- 1
=> n - 1 thuộc Ư ( 4 )
=> n - 1 thuộc { 1 ; 2 ; 4 }
=> n thuộc { 2 ; 3 ; 5 }