a) chứng minh \(\Delta ABC=\Delta ADC\)

xét 2 tam giác vuông ABC và ADC:

có AC: cạnh chung

AD=AB (gia thiết) 

=> \(\Delta ABC=\Delta ADC\) (2cgv)

b) chứng minh DC//BE

xét tứ giác BEDC có 2 đường chéo BD và EC cắt nhau tại trung điểm A của mỗi đường => tứ giác BEDC là hình bình hành => DC//BE

c) chứng minh BE = 2AI

ta có BEDC là hình bình hành => BE=DC

lại có tam giác DAC vuông tại A => đường trung tuyến AI bằng một nửa cạnh huyền, tức là \(AI=\dfrac{1}{2}DC\) hay \(DC=2.AI\) hay \(BE=2.AI\)

chúc em học tốt

a) Khôn nhà dại chợ

b) Nắng chóng trưa Mưa chóng tối

c) Áo rách khéo vá hơn lành vụng may

d) Cày sâu cuốc bẫm

\(y'=x^2+2mx+2m-1\)

hàm số đã cho có cực trị \(\Leftrightarrow\) \(y'=x^2+2mx+2m-1=0\) có 2 nghiệm phân biệt

\(\Leftrightarrow\Delta y'=4m^2-4\left(2m-1\right)=4m^2-8m+4>0\) hay \(m\ne1\)

hàm số đã cho xác định và liên tục trên đoạn \(\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]\)

f'(x) = 2 - 2sin(2x) = 0 => sin(2x) = 1 => \(x=\dfrac{\pi}{4}\in\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]\text{​​​​}\)

ta có: \(f\left(\dfrac{\pi}{12}\right)=\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2}< f\left(\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)

vậy \(\max\limits_{x\in\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]}y=f\left(\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)

=> C

a) ta có M, E lần lượt là trung điểm AB, AC => ME là đường trung bình của tam giác ABC => ME // BC (tính chất đường trung bình trong tam giác)

b) ME là đường trung bình của tam giác ABC (chminh câu a) => ME // BC và ME = 1/2 BC = PC (do P là trung điểm BC nên BP = PC = BC / 2)

tứ giác MECP có 2 cạnh đối diện ME song song và bằng cạnh CP => MECP là hình bình hành.

c) kéo dài AO (hay AI) cắt BC tại N

trong tam giác ANC ta có OE // NC (ME // BC)

và E là trung điểm AC (giả thuyết)

=> OE là đường trung bình tam giác ANC (định lí đường trung bình trong tam giác)

=> O là trung điểm của AN => AO = ON (1)

I là giao điểm 2 đường chéo MC và EP của hình bình hành MECP => EI = IP => tam giác OEI = tam giác NPI (g-c-g) => OI = NI (cạnh tương ứng) mà 3 điểm ONI thẳng hàng => I là trung điểm ON => ON = 2.OI (2)

Thế (2) vào (1) ta được AO = 2.OI (đpcm)

~chúc e học tốt!~

a) Bán kính của hình tròn (bằng đường kính chia cho 2): 7,2 : 2 = 3,6 (dm)

b) Chu vi hình tròn (bằng đường kính nhân với 3,14 hoặc bán kính nhân 2 rồi nhân với 3,14) : 7,2 x 3,14 = 22,608 (dm)

c) Diện tích hình tròn (bằng 3,14 nhân với bình phương của bán kính): 3,14 x 3,6 x 3,6 = 40,6944 (dm²)

~Chúc e học tốt!~

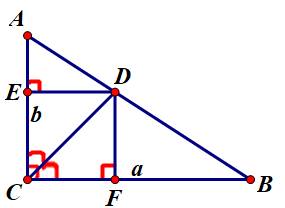
gọi E, F lần lượt là chân đường vuông góc hạ từ D xuống AC, CB.

tứ giác DECF có 3 góc vuông và CD là phân giác góc \(\widehat{ECF}\) 

=> DECF là hình vuông

gọi x (đvđd) là cạnh hình vuông DECF, CD là đường chéo hình vuông => CD = \(x\sqrt{2}\) (đvđd)

theo Talet: \(\dfrac{BF}{BC}=\dfrac{DF}{AC}\)hay \(\dfrac{a-x}{a}=\dfrac{x}{b}\Rightarrow ba-bx=ax\Rightarrow ab=x\left(a+b\right)\Rightarrow x=\dfrac{ab}{a+b}\)=> \(CD=x\sqrt{2}=\dfrac{ab}{a+b}\sqrt{2}=\dfrac{ab}{\left(a+b\right).\sin45^o}\) (đpcm)