Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(P=x^2+4x+2xy+3y^2+5y+2017\)
\(=x^2+2xy+y^2+4y+4+4x+2y^2+y+\dfrac{1}{8}+\dfrac{16103}{8}\)
\(=\left(x+y+2\right)^2+2\left(y^2+\dfrac{y}{2}+\dfrac{1}{16}\right)+\dfrac{16103}{8}\)
\(=\left(x+y+2\right)^2+2\left(y+\dfrac{1}{4}\right)^2+\dfrac{16103}{8}\ge\dfrac{16103}{8}\)
Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}x=-\dfrac{7}{4}\\y=-\dfrac{1}{4}\end{matrix}\right.\)
b)\(Q=-x^2+4x-3y^2+6y+2017\)
\(=-x^2+4x-4-3y^2+6y+3+2024\)
\(=-\left(x^2-4x+4\right)-\left(3y^2-6y-3\right)+2024\)
\(=-\left(x-2\right)^2-3\left(y^2-2y-1\right)+2024\)
\(=-\left(x-2\right)^2-3\left(y-1\right)^2+2024\ge2024\)
Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Ta có:
\(P=x^2+4x+2xy+3y^2+5y+2017\)
\(=x^2+2x\left(y+2\right)+\left(y+2\right)^2+2y^2+y+2013\)
\(=\left[x+\left(y+2\right)\right]^2+2\left(y^2+y+0,25\right)+2012,5\)
\(=\left(x+y+2\right)^2+2\left(y+0,5\right)^2+2012,5\ge2012,5\)
Dấu "=" xảy ra khi:
\(\Leftrightarrow\left\{{}\begin{matrix}x+y+2=0\\y+0,5=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=-0,5\\x=-1,5\end{matrix}\right.\)
Vậy \(minP=2012,5\) khi \(\left\{{}\begin{matrix}y=-0,5\\x=-1,5\end{matrix}\right.\)
Ta có:
\(Q=-x^2+4x-3y^2+6y+2017\)
\(=-\left(x^2-4x+4\right)-3\left(y^2-2y+1\right)+2024\)
\(=-\left(x-2\right)^2-3\left(y-1\right)^2+2024\le2024\)
Dấu "=" xảy ra khi \(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\y-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy \(maxQ=2024\) khi \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

a ) \(x^2-x+1\)
\(\Leftrightarrow\left(x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right)+\dfrac{3}{4}\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Ta có : \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Vậy GTNN là \(\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}.\)

\(A=3x^2+5x-2\)
\(A=3\left(x^2+\frac{5}{3}x-\frac{2}{3}\right)\)
\(A=3\left(x^2+2.\frac{5}{6}x+\left(\frac{5}{6}\right)^2-\frac{49}{36}\right)\)
\(A=3\left(x^2+2.\frac{5}{6}x+\left(\frac{5}{6}\right)^2\right)-\frac{49}{12}\)
\(A=3\left(x+\frac{5}{6}\right)^2-\frac{49}{12}\)
Vì \(3\left(x+\frac{5}{6}\right)^2\ge0\)
Do đó \(3\left(x+\frac{5}{6}\right)^2-\frac{49}{12}\ge-\frac{49}{12}\)
Dấu = xảy ra khi \(x+\frac{5}{6}=0\Rightarrow x=-\frac{5}{6}\)
Vậy Min A=\(-\frac{49}{12}\) khi x=\(-\frac{5}{6}\)
mk làm ý a thôi, mấy ý sau dựa vào mà làm.
A = \(3x^2+5x-2\)
=> \(\frac{A}{3}=x^2+\frac{5}{3}x-\frac{2}{3}\)(chia cả 2 vế cho 3)
\(\Leftrightarrow\frac{A}{3}=x^2+2.x.\frac{5}{6}+\left(\frac{5}{6}\right)^2-\frac{49}{36}\)
\(\Leftrightarrow\frac{A}{3}=\left(x+\frac{5}{6}\right)^2-\frac{49}{36}\)
\(\Rightarrow A=3\left(x+\frac{5}{6}\right)^2-\frac{49}{12}\ge-\frac{49}{12}\)
Đẳng thức xảy ra <=> x = - 5/6.
Vậy Min A = - 49/12 khi và chỉ khi x = - 5/6.

a, TK: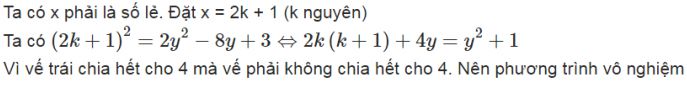
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương

Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.

\(x^2+2xy+4x+4y+3y^2+3=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(4x+4y\right)+4+2y^2-1=0\)
\(\Leftrightarrow\left(x+y\right)^2+4\left(x+y\right)+4=1-2y^2\)
\(\Leftrightarrow\left(x+y+2\right)^2=1-2y^2\)
Do \(VP=1-2y^2\le1\forall y\) nên \(VT=\left(x+y+2\right)^2\le1\)
\(\Leftrightarrow-1\le x+y+2\le1\)
\(\Leftrightarrow-1+2015\le x+y+2+2015\le1+2015\)
\(\Leftrightarrow2014\le x+y+2017\le2016\)
Hay \(2014\le B\le2016\)
câu A thiếu đề
B=\(x^2-2x+2017=\left(x-1\right)^2+2016>=2016\)
Min B=2016 khi x-1=0<=>x=1
+)D=\(-2x^2+4x+2017=-2\left(x^2-2x+1\right)+2019=-2\left(x-1\right)^2+2019< =2019\)
=>Max D=2019, dấu '=' xảy ra khi x-1=0<=>x=1
Bổ sung câu A. \(A=x^2+2xy+3y^2-4y+2017\)